Number of pairs such that path between pairs has the two vertices A and B
Last Updated :
05 Dec, 2021
Given an undirected connected graph and two vertices A and B, the task is to find the number of pairs of vertices {X, Y} such that any path from X to Y contains both vertices A and B.
Note:
- { X, Y } is treated equivalent to { Y, X }.
- X != A, X != B, Y != A and Y != B.
Examples:

For the above graph:
Input: A = 3, B = 5
Output:4
Explanation:
There are four pairs { X, Y } such that all the paths from the source X to the destination Y contain the vertices A, B. They are:
{1, 6}, {1, 7}, {2, 6} and {2, 7}.

For the above graph:
Input: A = 2, B = 1
Output: 1
Explanation:
There is only one pair { X, Y } such that all the paths from the source X to the destination Y contain the vertices A, B. That is:
{4, 3}.
Approach:
- For the given graph, if for any pair {X, Y}, if some other path exists between them apart from the given vertices A and B, then those two vertices are not included in the final answer. That is because we need the count of pairs such that any path from those pairs consists the vertices A and B.
- Therefore, we are interested in pairs of vertices { X, Y } such that deleting the vertex A(while going from B) breaks the connection from X to Y and deleting the vertex B(while going from A) breaks the connection from X to Y.
- In other words the pair {X, Y} interests us if X and Y belong to the different components of the graph both when removing A and when removing B.
Therefore, in order to find the above pairs, the following steps are followed:
- Consider a random directed connected graph where some group of nodes which are interconnected is connected to A and some group of interconnected nodes are connected to B. A and B may or may not have nodes between them.
- What if we remove both A and B? Then the graph can either become disconnected or remain connected.
- If the graph remains connected, then no pair of vertices exists because there are other paths in the graph for all the pairs {X, Y} without the vertices A and B in it.
- If the graph becomes disconnected, then there arise two cases:
- On removing vertices A and B, the graph is converted to two disconnected components.
- On removing vertices A and B, the graph is converted to three disconnected components.
If on removing vertices A and B, the graph is converted to two disconnected components, then three cases arise:
- When there is a group of interconnected nodes connected to the vertex A, some independent nodes are connected to A and B and the vertex B is the leaf node of the graph:
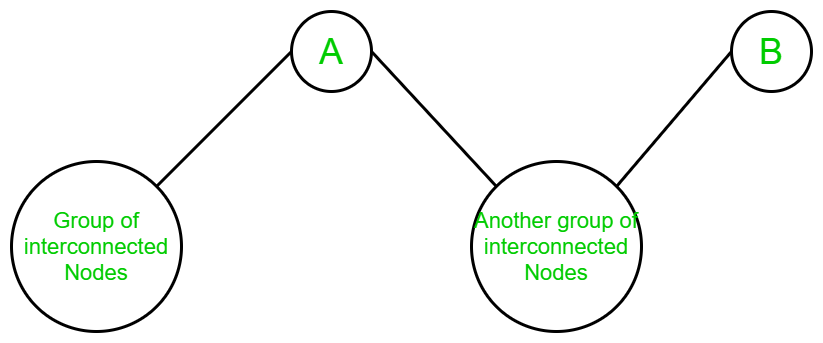
- Clearly, in the above graph, the graph is converted into two different components when vertex A and vertex B is removed from it. And, any component can be discarded because vertices of one component may go to vertices of any other component without traversing through vertex B. So no pair exists.
- When there is a group of interconnected nodes connected to the vertex B, some independent nodes are connected to A and B and the vertex A is the leaf node of the graph:

- Clearly, in the above graph, the graph is converted into two different components when vertex A and vertex B is removed from it. And, any component can be discarded because vertices of one component may go to vertices of any other component without traversing through vertex A. So no pair exists.
- When there are no nodes between vertex A and vertex B and neither of the vertices A and B are the leaf nodes of the graph:

- Clearly, in the above graph, the graph is converted into two different components when vertex A and vertex B is removed from it. Here, any one of the vertex of one component can be paired up with any vertex of the other component. Therefore, the number of pairs in this graph becomes the product of the count of number of interconnected nodes in component 1 and component two.
If on removing vertices A and B, the graph is converted to three disconnected components, then only one case arises:
- When there is a group of interconnected nodes connected to vertex A, vertex B and there is another group of nodes between vertex A and vertex B and none of the vertices A and B are the leaf nodes:

- In this case, the component between vertex A and B can be discarded due to the above-mentioned reasons. And, once its discarded, it is directly the case 3 in the two-component graph. The same concept is applied to find the number of vertices.
Therefore, the above idea is implemented in the following steps:
- Store the graph as adjacency list by using vector STL.
- Run DFS such that we fix the vertex B as if we removed it. This can be done using base condition of the DFS function i.e. the call is returned on reaching the vertex B.
- Count the vertices that can not be reached by A after removing B.
- Repeat the above two steps by fixing the vertex A and counting the number of vertices that cannot be reached by B after removing the vertex A.
- Store both counts in two different variables. This represents the count of vertices set first on removing B and then removing A.
- Multiplying both the counts is the required answer.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int cnt, num_vertices, num_edges, a, b;
void dfs(int a, int b, vector<int> v[], int vis[])
{
vis[a] = 1;
cnt++;
for (auto i : v[a]) {
if (!vis[i] && i != b)
dfs(i, b, v, vis);
}
}
void Calculate(vector<int> v[])
{
int vis[num_vertices + 1];
memset(vis, 0, sizeof(vis));
cnt = 0;
dfs(a, b, v, vis);
int ans1 = num_vertices - cnt - 1;
memset(vis, 0, sizeof(vis));
cnt = 0;
dfs(b, a, v, vis);
int ans2 = num_vertices - cnt - 1;
cout << ans1 * ans2 << "\n";
}
int main()
{
num_vertices = 7, num_edges = 7, a = 3, b = 5;
int edges[][2] = { { 1, 2 },
{ 2, 3 },
{ 3, 4 },
{ 4, 5 },
{ 5, 6 },
{ 6, 7 },
{ 7, 5 } };
vector<int> v[num_vertices + 1];
for (int i = 0; i < num_edges; i++) {
v[edges[i][0]].push_back(edges[i][1]);
v[edges[i][1]].push_back(edges[i][0]);
}
Calculate(v);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int N = 1000001;
static int c, n, m, a, b;
static void dfs(int a, int b, Vector<Integer> v[], int vis[])
{
vis[a] = 1;
c++;
for (int i : v[a]) {
if (vis[i] == 0 && i != b)
dfs(i, b, v, vis);
}
}
static void Calculate(Vector<Integer> v[])
{
int []vis = new int[n + 1];
Arrays.fill(vis, 0);
c = 0;
dfs(a, b, v, vis);
int ans1 = n - c - 1;
Arrays.fill(vis, 0);
c = 0;
dfs(b, a, v, vis);
int ans2 = n - c - 1;
System.out.print(ans1 * ans2+ "\n");
}
public static void main(String[] args)
{
n = 7;
m = 7;
a = 3;
b = 5;
int edges[][] = { { 1, 2 },
{ 2, 3 },
{ 3, 4 },
{ 4, 5 },
{ 5, 6 },
{ 6, 7 },
{ 7, 5 } };
Vector<Integer> []v = new Vector[n + 1];
for(int i= 0; i <= n; i++) {
v[i] = new Vector<Integer>();
}
for (int i = 0; i < m; i++) {
v[edges[i][0]].add(edges[i][1]);
v[edges[i][1]].add(edges[i][0]);
}
Calculate(v);
}
}
|
Python3
N = 1000001
c = 0
n = 0
m = 0
a = 0
b = 0
def dfs(a,b,v,vis):
global c
vis[a] = 1
c += 1
for i in v[a]:
if (vis[i]==0 and i != b):
dfs(i, b, v, vis)
def Calculate(v):
global c
vis = [0 for i in range(n + 1)]
c = 0
dfs(a, b, v, vis)
ans1 = n - c - 1
vis = [0 for i in range(len(vis))]
c = 0
dfs(b, a, v, vis)
ans2 = n - c - 1
print(ans1 * ans2)
if __name__ == '__main__':
n = 7
m = 7
a = 3
b = 5
edges = [[1, 2], [2, 3], [3, 4], [4, 5], [5, 6], [6, 7], [7, 5]]
v = [[] for i in range(n + 1)]
for i in range(m):
v[edges[i][0]].append(edges[i][1])
v[edges[i][1]].append(edges[i][0])
Calculate(v)
|
C#
using System;
using System.Collections.Generic;
class GFG{
static int N = 1000001;
static int c, n, m, a, b;
static void dfs(int a, int b, List<int> []v, int []vis)
{
vis[a] = 1;
c++;
foreach (int i in v[a]) {
if (vis[i] == 0 && i != b)
dfs(i, b, v, vis);
}
}
static void Calculate(List<int> []v)
{
int []vis = new int[n + 1];
for(int i = 0; i < n + 1; i++)
vis[i] = 0;
c = 0;
dfs(a, b, v, vis);
int ans1 = n - c - 1;
for(int i = 0; i < n + 1; i++)
vis[i] = 0;
c = 0;
dfs(b, a, v, vis);
int ans2 = n - c - 1;
Console.Write(ans1 * ans2+ "\n");
}
public static void Main(String[] args)
{
n = 7;
m = 7;
a = 3;
b = 5;
int [,]edges = { { 1, 2 },
{ 2, 3 },
{ 3, 4 },
{ 4, 5 },
{ 5, 6 },
{ 6, 7 },
{ 7, 5 } };
List<int> []v = new List<int>[n + 1];
for(int i= 0; i <= n; i++) {
v[i] = new List<int>();
}
for (int i = 0; i < m; i++) {
v[edges[i,0]].Add(edges[i,1]);
v[edges[i,1]].Add(edges[i,0]);
}
Calculate(v);
}
}
|
Javascript
<script>
let N = 1000001;
let c, n, m, a, b;
function dfs(a, b, v, vis)
{
vis[a] = 1;
c++;
for(let i of v[a]) {
if (vis[i] == 0 && i != b)
dfs(i, b, v, vis);
}
}
function Calculate(v)
{
let vis = new Array(n + 1);
for(let i = 0; i < n + 1; i++)
vis[i] = 0;
c = 0;
dfs(a, b, v, vis);
let ans1 = n - c - 1;
for(let i = 0; i < n + 1; i++)
vis[i] = 0;
c = 0;
dfs(b, a, v, vis);
let ans2 = n - c - 1;
document.write((ans1 * ans2)+ "</br>");
}
n = 7;
m = 7;
a = 3;
b = 5;
let edges = [ [ 1, 2 ],
[ 2, 3 ],
[ 3, 4 ],
[ 4, 5 ],
[ 5, 6 ],
[ 6, 7 ],
[ 7, 5 ] ];
let v = new Array(n + 1);
for(let i= 0; i <= n; i++) {
v[i] = [];
}
for (let i = 0; i < m; i++) {
v[edges[i][0]].push(edges[i][1]);
v[edges[i][1]].push(edges[i][0]);
}
Calculate(v);
</script>
|
Time Complexity Analysis:
- Here, DFS is performed twice. Therefore, the overall time complexity is O(V + E).
Auxiliary Space : O(V + E)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...