Number of connected components of a graph ( using Disjoint Set Union )
Last Updated :
19 Apr, 2024
Given an undirected graph G with vertices numbered in the range [0, N] and an array Edges[][] consisting of M edges, the task is to find the total number of connected components in the graph using Disjoint Set Union algorithm.
Examples:
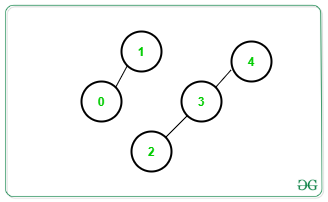
Input: N = 4, Edges[][] = {{1, 0}, {2, 3}, {3, 4}}
Output: 2
Explanation: There are only 2 connected components as shown below:
Input: N = 7, Edges[][] = {{1, 0}, {0, 2}, {3, 5}, {3, 4}, {6, 7}}
Output: 3
Explanation: There are only 3 connected components as shown below:

Approach: The problem can be solved using Disjoint Set Union algorithm. Follow the steps below to solve the problem:
- In DSU algorithm, there are two main functions, i.e. connect() and root() function.
- connect(): Connects an edge.
- root(): Recursively determine the topmost parent of a given edge.
- For each edge {a, b}, check if a is connected to b or not. If found to be false, connect them by appending their top parents.
- After completing the above step for every edge, print the total number of the distinct top-most parents for each vertex.
Below is the implementation of the above approach:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Stores the parent of each vertex
int parent[1000000];
// Function to find the topmost
// parent of vertex a
int root(int a)
{
// If current vertex is
// the topmost vertex
if (a == parent[a]) {
return a;
}
// Otherwise, set topmost vertex of
// its parent as its topmost vertex
return parent[a] = root(parent[a]);
}
// Function to connect the component
// having vertex a with the component
// having vertex b
void connect(int a, int b)
{
// Connect edges
a = root(a);
b = root(b);
if (a != b) {
parent[b] = a;
}
}
// Function to find unique top most parents
void connectedComponents(int n)
{
set<int> s;
// Traverse all vertices
for (int i = 0; i < n; i++) {
// Insert all topmost
// vertices obtained
s.insert(root(parent[i]));
}
// Print count of connected components
cout << s.size() << '\n';
}
// Function to print answer
void printAnswer(int N,
vector<vector<int> > edges)
{
// Setting parent to itself
for (int i = 0; i <= N; i++) {
parent[i] = i;
}
// Traverse all edges
for (int i = 0; i < edges.size(); i++) {
connect(edges[i][0], edges[i][1]);
}
// Print answer
connectedComponents(N);
}
// Driver Code
int main()
{
// Given N
int N = 8;
// Given edges
vector<vector<int> > edges = {
{ 1, 0 }, { 0, 2 }, { 5, 3 }, { 3, 4 }, { 6, 7 }
};
// Function call
printAnswer(N, edges);
return 0;
}
import java.util.*;
class GFG {
// Stores the parent of each vertex
static int[] parent = new int[1000000];
// Function to find the topmost parent of vertex a
static int root(int a) {
if (a == parent[a]) {
return a;
}
return parent[a] = root(parent[a]);
}
// Function to connect the component having vertex a with the component having vertex b
static void connect(int a, int b) {
a = root(a);
b = root(b);
if (a != b) {
parent[b] = a;
}
}
// Function to find unique top most parents
static void connectedComponents(int n) {
HashSet<Integer> s = new HashSet<Integer>();
// Traverse all vertices
for (int i = 0; i < n; i++) {
// Insert all topmost vertices obtained
s.add(root(i));
}
// Print count of connected components
System.out.println(s.size());
}
// Function to print answer
static void printAnswer(int N, int[][] edges) {
// Setting parent to itself
for (int i = 0; i <= N; i++) {
parent[i] = i;
}
// Traverse all edges
for (int i = 0; i < edges.length; i++) {
connect(edges[i][0], edges[i][1]);
}
// Print answer
connectedComponents(N);
}
// Driver Code
public static void main(String[] args) {
// Given N
int N = 8;
// Given edges
int[][] edges = { { 0, 1 }, { 0, 2 }, { 0, 3 }, { 4, 5 }, { 4, 6 }, { 4, 0 } };
// Function call
printAnswer(N, edges);
}
}
# Python3 program for the above approach
from collections import defaultdict
# Given N
N = 8
# Given edges
edges = [[1, 0 ], [ 0, 2 ], [ 5, 3 ], [ 3, 4 ], [ 6, 7 ]]
# Stores the parent of each vertex
parent = list(range(N))
# Function to find the topmost
# parent of vertex x
def find(x):
if x != parent[x]:
parent[x] = find(parent[x])
return parent[x]
def union(x,y):
parent_x = find(x)
parent_y = find(y)
if parent_x != parent_y:
parent[parent_y] = parent_x
for x,y in edges:
union(x,y)
dict_pair = defaultdict(list)
for idx, val in enumerate(parent):
dict_pair[find(val)].append(idx)
print(len(dict_pair.keys()))
# This code is contributed by Shivam Dwivedi
// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG {
// Stores the parent of each vertex
static int[] parent = new int[1000000];
// Function to find the topmost
// parent of vertex a
static int root(int a)
{
// If current vertex is
// the topmost vertex
if (a == parent[a]) {
return a;
}
// Otherwise, set topmost vertex of
// its parent as its topmost vertex
return parent[a] = root(parent[a]);
}
// Function to connect the component
// having vertex a with the component
// having vertex b
static void connect(int a, int b)
{
// Connect edges
a = root(a);
b = root(b);
if (a != b) {
parent[b] = a;
}
}
// Function to find unique top most parents
static void connectedComponents(int n)
{
HashSet<int> s = new HashSet<int>();
// Traverse all vertices
for (int i = 0; i < n; i++) {
// Insert all topmost
// vertices obtained
s.Add(parent[i]);
}
// Print count of connected components
Console.WriteLine(s.Count);
}
// Function to print answer
static void printAnswer(int N, List<List<int> > edges)
{
// Setting parent to itself
for (int i = 0; i <= N; i++) {
parent[i] = i;
}
// Traverse all edges
for (int i = 0; i < edges.Count; i++) {
connect(edges[i][0], edges[i][1]);
}
// Print answer
connectedComponents(N);
}
// Driver code
static void Main() {
// Given N
int N = 8;
// Given edges
List<List<int>> edges = new List<List<int>>();
edges.Add(new List<int> { 1, 0 });
edges.Add(new List<int> { 0, 2 });
edges.Add(new List<int> { 5, 3 });
edges.Add(new List<int> { 3, 4 });
edges.Add(new List<int> { 6, 7 });
// Function call
printAnswer(N, edges);
}
}
// This code is contributed by divyeshrabadiya07
<script>
// Javascript program for the above approach
// Stores the parent of each vertex
var parent = Array(1000000);
// Function to find the topmost
// parent of vertex a
function root(a)
{
// If current vertex is
// the topmost vertex
if (a == parent[a]) {
return a;
}
// Otherwise, set topmost vertex of
// its parent as its topmost vertex
return parent[a] = root(parent[a]);
}
// Function to connect the component
// having vertex a with the component
// having vertex b
function connect( a, b)
{
// Connect edges
a = root(a);
b = root(b);
if (a != b) {
parent[b] = a;
}
}
// Function to find unique top most parents
function connectedComponents( n)
{
var s = new Set();
// Traverse all vertices
for (var i = 0; i < n; i++) {
// Insert all topmost
// vertices obtained
s.add(parent[i]);
}
// Print count of connected components
document.write( s.size + "<br>");
}
// Function to print answer
function printAnswer( N, edges)
{
// Setting parent to itself
for (var i = 0; i <= N; i++) {
parent[i] = i;
}
// Traverse all edges
for (var i = 0; i < edges.length; i++) {
connect(edges[i][0], edges[i][1]);
}
// Print answer
connectedComponents(N);
}
// Driver Code
// Given N
var N = 8;
// Given edges
var edges = [
[ 1, 0 ], [ 0, 2 ], [ 5, 3 ], [ 3, 4 ], [ 6, 7 ]
];
// Function call
printAnswer(N, edges);
</script>
Time Complexity: O(NLOGN+M)
Auxiliary Space: O(N+M)
Share your thoughts in the comments
Please Login to comment...