Calculate number of nodes between two vertices in an acyclic Graph by Disjoint Union method

Given a connected acyclic graph, a source vertex and a destination vertex, your task is to count the number of vertices between the given source and destination vertex by Disjoint Union Method .

Examples:

Input : 1 4
        4 5
        4 2
        2 6
        6 3
        1 3 
Output : 3
In the input 6 is the total number of vertices
labeled from 1 to 6 and the next 5 lines are the connection 
between vertices. Please see the figure for more
explanation. And in last line 1 is the source vertex
and 3 is the destination vertex. From the figure 
it is clear that there are 3 nodes(4, 2, 6) present
between 1 and 3. 

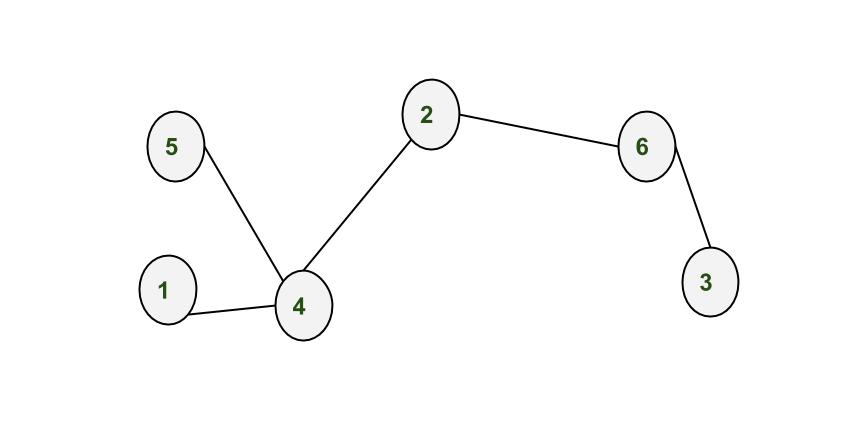
To use the disjoint union method we have to first check the parent of each of the node of the given graph. We can use BFS to traverse through the graph and calculate the parent vertex of each vertices of graph. For example, if we traverse the graph (i.e starts our BFS) from vertex 1 then 1 is the parent of 4, then 4 is the parent of 5 and 2, again 2 is the parent of 6 and 6 is the parent of 3.

Now to calculate the number of nodes between the source node and destination node, we have to make a loop that starts with parent of the destination node and after every iteration we will update this node with parent of current node, keeping the count of the number of iterations. The execution of the loop will terminate when we reach the source vertex and the count variable gives the number of nodes in the connection path of the source node and destination node. 

In the above method, the disjoint sets are all the sets with a single vertex, and we have used union operation to merge two sets where one contains the parent node and other contains the child node.

Below are implementations of above approach.

C++

// C++ program to calculate number
// of nodes between two nodes
#include <bits/stdc++.h>
using namespace std;

// function to calculate no of nodes
// between two nodes
int totalNodes(vector<int> adjac[], int n,
                             int x, int y)
{
    // x is the source node and
    // y is destination node

    // visited array take account of
    // the nodes visited through the bfs
    bool visited[n+1] = {0};

    // parent array to store each nodes
    // parent value
    int p[n] ;

    queue<int> q;
    q.push(x);

    // take our first node(x) as first element
    // of queue and marked it as
    // visited through visited[] array
    visited[x] = true;

    int m;

    // normal bfs method starts
    while (!q.empty())
    {
        m = q.front() ;
        q.pop();
        for (int i=0; i<adjac[m].size(); ++i)
        {
            int h = adjac[m][i];
            if (!visited[h])
            {
                visited[h] = true;

                // when new node is encountered
                // we assign it's parent value
                // in parent array p
                p[h] = m ;
                q.push(h);
            }
        }
    }

    // count variable stores the result
    int count = 0;

    // loop start with parent of y
    // till we encountered x
    int i = p[y];
    while (i != x)
    {
        // count increases for counting
        // the nodes
        count++;

        i = p[i];
    }

    return count ;
}

// Driver program to test above function
int main()
{
    // adjacency list for graph
    vector < int > adjac[7];

    // creating graph, keeping length of
    // adjacency list as (1 + no of nodes)
    // as index ranges from (0 to n-1)
    adjac[1].push_back(4);
    adjac[4].push_back(1);
    adjac[5].push_back(4);
    adjac[4].push_back(5);
    adjac[4].push_back(2);
    adjac[2].push_back(4);
    adjac[2].push_back(6);
    adjac[6].push_back(2);
    adjac[6].push_back(3);
    adjac[3].push_back(6);

    cout << totalNodes(adjac, 7, 1, 3);

    return 0;
}

Java

// Java program to calculate number
// of nodes between two nodes
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Vector;

public class GFG
{
    // function to calculate no of nodes
    // between two nodes
    static int totalNodes(Vector<Integer> adjac[],
                            int n, int x, int y)
    {
        // x is the source node and
        // y is destination node

        // visited array take account of
        // the nodes visited through the bfs
        Boolean visited[] = new Boolean[n + 1];

        //filling boolean value with false
        Arrays.fill(visited, false);

        // parent array to store each nodes
        // parent value
        int p[] = new int[n];

        Queue<Integer> q = new LinkedList<>();
        q.add(x);


        // take our first node(x) as first element
        // of queue and marked it as
        // visited through visited[] array
        visited[x] = true;

        int m;

        // normal bfs method starts
        while(!q.isEmpty())
        {
            m = q.peek();
            q.poll();
            for(int i=0; i < adjac[m].size() ; ++i)
            {

                int h = adjac[m].get(i);

                if(visited[h] != true )
                {
                    visited[h] = true;

                    // when new node is encountered
                    // we assign it's parent value
                    // in parent array p
                    p[h] = m;
                    q.add(h);
                }
            }
        }

        // count variable stores the result
        int count  = 0;

        // loop start with parent of y
        // till we encountered x
        int i = p[y];
        while(i != x)
        {
            // count increases for counting
            // the nodes
            count++;
            i = p[i];
        }
        return count;
    }

    // Driver program to test above function
    public static void main(String[] args)
    {
        // adjacency list for graph
        Vector<Integer> adjac[] = new Vector[7];

        //Initializing Vector for each nodes
        for (int i = 0; i < 7; i++)
            adjac[i] = new Vector<>();

        // creating graph, keeping length of
        // adjacency list as (1 + no of nodes)
        // as index ranges from (0 to n-1)
        adjac[1].add(4);
        adjac[4].add(1);
        adjac[5].add(4);
        adjac[4].add(5);
        adjac[4].add(2);
        adjac[2].add(4);
        adjac[2].add(6);
        adjac[6].add(2);
        adjac[6].add(3);
        adjac[3].add(6);

        System.out.println(totalNodes(adjac, 7, 1, 3));

    }
}
// This code is contributed by Sumit Ghosh

Python3

# Python3 program to calculate number
# of nodes between two nodes
import queue

# function to calculate no of nodes
# between two nodes
def totalNodes(adjac, n, x, y):

    # x is the source node and
    # y is destination node

    # visited array take account of
    # the nodes visited through the bfs
    visited = [0] * (n + 1)

    # parent array to store each nodes
    # parent value
    p = [None] * n

    q = queue.Queue()
    q.put(x)

    # take our first node(x) as first
    # element of queue and marked it as
    # visited through visited[] array
    visited[x] = True

    m = None

    # normal bfs method starts
    while (not q.empty()):
        m = q.get()
        for i in range(len(adjac[m])):
            h = adjac[m][i]
            if (not visited[h]):
                visited[h] = True

                # when new node is encountered
                # we assign it's parent value
                # in parent array p
                p[h] = m
                q.put(h)

    # count variable stores the result
    count = 0

    # loop start with parent of y
    # till we encountered x
    i = p[y]
    while (i != x):

        # count increases for counting
        # the nodes
        count += 1

        i = p[i]

    return count

# Driver Code
if __name__ == '__main__':

    # adjacency list for graph
    adjac = [[] for i in range(7)]

    # creating graph, keeping length of
    # adjacency list as (1 + no of nodes)
    # as index ranges from (0 to n-1)
    adjac[1].append(4)
    adjac[4].append(1)
    adjac[5].append(4)
    adjac[4].append(5)
    adjac[4].append(2)
    adjac[2].append(4)
    adjac[2].append(6)
    adjac[6].append(2)
    adjac[6].append(3)
    adjac[3].append(6)

    print(totalNodes(adjac, 7, 1, 3))

# This code is contributed by PranchalK

C#

// C# program to calculate number
// of nodes between two nodes
using System;
using System.Collections.Generic;

class GFG
{
    // function to calculate no of nodes
    // between two nodes
    static int totalNodes(List<int> []adjac,
                          int n, int x, int y)
    {
        // x is the source node and
        // y is destination node

        // visited array take account of
        // the nodes visited through the bfs
        Boolean []visited = new Boolean[n + 1];


        // parent array to store each nodes
        // parent value
        int []p = new int[n];

        Queue<int> q = new Queue<int>();
        q.Enqueue(x);


        // take our first node(x) as first element
        // of queue and marked it as
        // visited through visited[] array
        visited[x] = true;

        int m, i;

        // normal bfs method starts
        while(q.Count != 0)
        {
            m = q.Peek();
            q.Dequeue();
            for(i = 0; i < adjac[m].Count ; ++i)
            {
                int h = adjac[m][i];

                if(visited[h] != true )
                {
                    visited[h] = true;

                    // when new node is encountered
                    // we assign it's parent value
                    // in parent array p
                    p[h] = m;
                    q.Enqueue(h);
                }
            }
        }

        // count variable stores the result
        int count = 0;

        // loop start with parent of y
        // till we encountered x
        i = p[y];
        while(i != x)
        {
            // count increases for counting
            // the nodes
            count++;
            i = p[i];
        }
        return count;
    }

    // Driver Code
    public static void Main(String[] args)
    {
        // adjacency list for graph
        List<int> []adjac = new List<int>[7];

        //Initializing Vector for each nodes
        for (int i = 0; i < 7; i++)
            adjac[i] = new List<int>();

        // creating graph, keeping length of
        // adjacency list as (1 + no of nodes)
        // as index ranges from (0 to n-1)
        adjac[1].Add(4);
        adjac[4].Add(1);
        adjac[5].Add(4);
        adjac[4].Add(5);
        adjac[4].Add(2);
        adjac[2].Add(4);
        adjac[2].Add(6);
        adjac[6].Add(2);
        adjac[6].Add(3);
        adjac[3].Add(6);

        Console.WriteLine(totalNodes(adjac, 7, 1, 3));
    }
}

// This code is contributed by 29AjayKumar

Javascript

<script>
// Javascript program to calculate number
// of nodes between two nodes

// function to calculate no of nodes
    // between two nodes
function totalNodes(adjac,n,x,y)
{
     // x is the source node and
        // y is destination node

        // visited array take account of
        // the nodes visited through the bfs
        let visited = new Array(n + 1);

        // filling boolean value with false
        for(let i=0;i<n+1;i++)
        {
            visited[i]=false;
        }

        // parent array to store each nodes
        // parent value
        let p = new Array(n);

        let q = [];
        q.push(x);


        // take our first node(x) as first element
        // of queue and marked it as
        // visited through visited[] array
        visited[x] = true;

        let m;

        // normal bfs method starts
        while(q.length!=0)
        {
            m = q[0];
            q.shift();
            for(let i=0; i < adjac[m].length ; ++i)
            {

                let h = adjac[m][i];

                if(visited[h] != true )
                {
                    visited[h] = true;

                    // when new node is encountered
                    // we assign it's parent value
                    // in parent array p
                    p[h] = m;
                    q.push(h);
                }
            }
        }

        // count variable stores the result
        let count  = 0;

        // loop start with parent of y
        // till we encountered x
        let i = p[y];
        while(i != x)
        {
            // count increases for counting
            // the nodes
            count++;
            i = p[i];
        }
        return count;
}

// Driver program to test above function
let adjac = new Array(7);

//Initializing Vector for each nodes
for (let i = 0; i < 7; i++)
    adjac[i] = [];

// creating graph, keeping length of
// adjacency list as (1 + no of nodes)
// as index ranges from (0 to n-1)
adjac[1].push(4);
adjac[4].push(1);
adjac[5].push(4);
adjac[4].push(5);
adjac[4].push(2);
adjac[2].push(4);
adjac[2].push(6);
adjac[6].push(2);
adjac[6].push(3);
adjac[3].push(6);

document.write(totalNodes(adjac, 7, 1, 3));

// This code is contributed by rag2127
</script>

Output

3

Time Complexity: O(n), where n is total number of nodes in the graph.

Space complexity : O(n), where n is the number of nodes in the graph.

This article is contributed by Surya Priy. If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.