Number of n-digits non-decreasing integers
Last Updated :
15 Sep, 2023
Given an integer n > 0, which denotes the number of digits, the task to find the total number of n-digit positive integers which are non-decreasing in nature.
A non-decreasing integer is one in which all the digits from left to right are in non-decreasing form. ex: 1234, 1135, ..etc.
Note: Leading zeros also count in non-decreasing integers such as 0000, 0001, 0023, etc are also non-decreasing integers of 4-digits.
Examples :
Input : n = 1
Output : 10
Numbers are 0, 1, 2, ...9.
Input : n = 2
Output : 55
Input : n = 4
Output : 715
Naive Approach: We generate all possible n-digit numbers and then for each number we check whether it is non-decreasing or not.
Time Complexity : (n*10^n), where 10^n is for generating all possible n-digits numbers and n is for checking whether a particular number is non-decreasing or not.
Efficient Approach using dynamic Programming:
If we fill digits one by one from left to right, the following conditions hold.
- If current last digit is 9, we can fill only 9s in remaining places. So only one solution is possible if current last digit is 9.
- If current last digit is less than 9, then we can recursively compute count using following formula.
a[i][j] = a[i-1][j] + a[i][j + 1]
For every digit j smaller than 9.
We consider previous length count and count
to be increased by all greater digits.
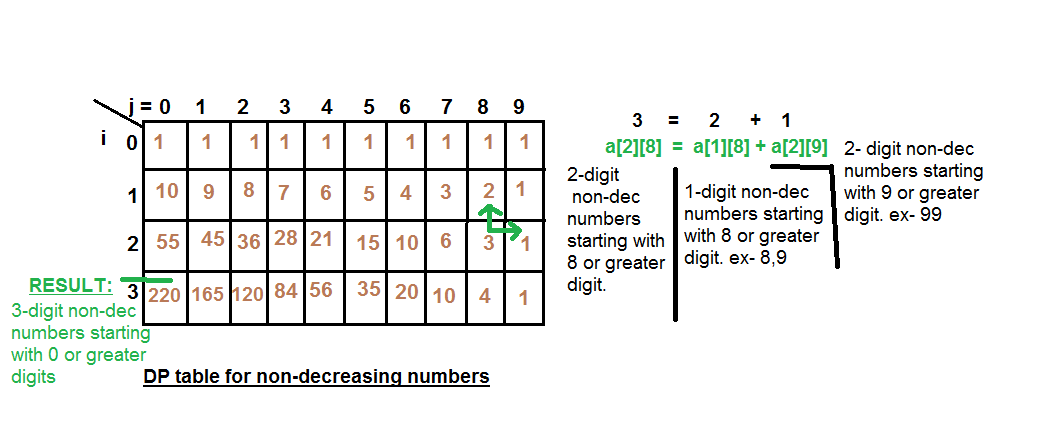
We build a matrix a[][] where a[i][j] = count of all valid i-digit non-decreasing integers with j or greater than j as the leading digit. The solution is based on below observations. We fill this matrix column-wise, first calculating a[1][9] then using this value to compute a[2][8] and so on.
At any instant if we wish to calculate a[i][j] means number of i-digits non-decreasing integers with leading digit as j or digit greater than j, we should add up a[i-1][j] (number of i-1 digit integers which should start from j or greater digit, because in this case if we place j as its left most digit then our number will be i-digit non-decreasing number) and a[i][j+1] (number of i-digit integers which should start with digit equals to greater than j+1). So, a[i][j] = a[i-1][j] + a[i][j+1].
 Below is the implementation of the above approach:
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int nonDecNums(int n)
{
int a[n + 1][10];
for (int i = 0; i <= 9; i++)
a[0][i] = 1;
for (int i = 1; i <= n; i++)
a[i][9] = 1;
for (int i = 1; i <= n; i++)
for (int j = 8; j >= 0; j--)
a[i][j] = a[i - 1][j] + a[i][j + 1];
return a[n][0];
}
int main()
{
int n = 2;
cout << "Non-decreasing digits = "
<< nonDecNums(n) << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
static int nonDecNums(int n)
{
int[][] a = new int[n + 1][10];
for (int i = 0; i <= 9; i++)
a[0][i] = 1;
for (int i = 1; i <= n; i++)
a[i][9] = 1;
for (int i = 1; i <= n; i++)
for (int j = 8; j >= 0; j--)
a[i][j] = a[i - 1][j] + a[i][j + 1];
return a[n][0];
}
public static void main(String[] args)
{
int n = 2;
System.out.println("Non-decreasing digits = " + nonDecNums(n));
}
}
|
Python3
import numpy as np
def nonDecNums(n) :
a = np.zeros((n + 1, 10))
for i in range(10) :
a[0][i] = 1
for i in range(1, n + 1) :
a[i][9] = 1
for i in range(1, n + 1) :
for j in range(8, -1, -1) :
a[i][j] = a[i - 1][j] + a[i][j + 1]
return int(a[n][0])
if __name__ == "__main__" :
n = 2
print("Non-decreasing digits = ",
nonDecNums(n))
|
C#
using System;
class GFG {
static int nonDecNums(int n)
{
int[, ] a = new int[n + 1, 10];
for (int i = 0; i <= 9; i++)
a[0, i] = 1;
for (int i = 1; i <= n; i++)
a[i, 9] = 1;
for (int i = 1; i <= n; i++)
for (int j = 8; j >= 0; j--)
a[i, j] = a[i - 1, j] + a[i, j + 1];
return a[n, 0];
}
public static void Main()
{
int n = 2;
Console.WriteLine("Non-decreasing digits = " +
nonDecNums(n));
}
}
|
PHP
<?php
function nonDecNums($n)
{
for ($i = 0; $i <= 9; $i++)
$a[0][$i] = 1;
for ($i = 1; $i <= $n; $i++)
$a[$i][9] = 1;
for ($i = 1; $i <= $n; $i++)
for ($j = 8; $j >= 0; $j--)
$a[$i][$j] = $a[$i - 1][$j] +
$a[$i][$j + 1];
return $a[$n][0];
}
$n = 2;
echo "Non-decreasing digits = ",
nonDecNums($n),"\n";
?>
|
Javascript
<script>
function nonDecNums(n)
{
let a = new Array(n + 1)
for (let i = 0; i < n + 1; i++)
{
a[i] = new Array(10);
}
for (let i = 0; i <= 9; i++)
a[0][i] = 1;
for (let i = 1; i <= n; i++)
a[i][9] = 1;
for (let i = 1; i <= n; i++)
for (let j = 8; j >= 0; j--)
a[i][j] = a[i - 1][j] + a[i][j + 1];
return a[n][0];
}
let n = 2;
document.write(
"Non-decreasing digits = " + nonDecNums(n)
);
</script>
|
Output
Non-decreasing digits = 55
Time Complexity : O(10*n) equivalent to O(n).
Another Approach:
If we observe, we can see that 0 has to be placed before 1-9, 1 has to be placed before 2-9 and so on. As we are asked to find non-decreasing integers, 111223 is a valid non-decreasing integer which means same digit can occur conscuetively.

Example 1: When N=2, we have 11C9, which is equal to 55.
Example 2: When N=5, we have 14C9, which is equal to 2002.
C++
#include <bits/stdc++.h>
using namespace std;
long long int fact(int n)
{
long long int res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
long long int nCr(int n, int r)
{
return fact(n) / (fact(r) * fact(n - r));
}
int main()
{
int n = 2;
cout <<"Number of Non-Decreasing digits: "<< nCr(n+9,9);
return 0;
}
|
Java
import java.io.*;
class GFG {
static long fact(int n)
{
long res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
static long nCr(int n, int r)
{
return fact(n) / (fact(r) * fact(n - r));
}
public static void main(String[] args)
{
int n = 2;
System.out.println(
"Number of Non-Decreasing digits: "
+ nCr(n + 9, 9));
}
}
|
Python3
def fact(n):
res = 1
for i in range (2,n+1):
res = res * i
return res
def nCr(n, r):
return fact(n) // ((fact(r) * fact(n - r)))
n = 2
print("Number of Non-Decreasing digits: " , nCr(n+9,9))
|
C#
using System;
class GFG {
static long fact(int n)
{
long res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
static long nCr(int n, int r)
{
return fact(n) / (fact(r) * fact(n - r));
}
public static void Main(String[] args)
{
int n = 2;
Console.Write("Number of Non-Decreasing digits: " + nCr(n + 9, 9));
}
}
|
Javascript
<script>
function fact( n)
{
var res = 1;
for (var i = 2; i <= n; i++)
res = res * i;
return res;
}
function nCr(n, r)
{
return fact(n) / (fact(r) * fact(n - r));
}
var n = 2;
document.write("Number of Non-Decreasing digits: " + nCr(n + 9, 9));
</script>
|
Output
Number of Non-Decreasing digits: 55
Time Complexity : O(n).
Auxiliary Space: O(n) .
Share your thoughts in the comments
Please Login to comment...