Number of digits in N factorial to the power N
Last Updated :
08 Sep, 2022
Given a positive integer N, we have to find the total number of digits in the factorial of N raised to the power N, i.e, 
Examples:
Input: 4
Output: 6
Explanations:  =
= 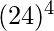 = 331776. Total number of digits in 331776 is 6.Input: 5Output: 11Explanations:
= 331776. Total number of digits in 331776 is 6.Input: 5Output: 11Explanations:  =
= 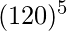 = 24883200000Total number of digits in 24883200000 is 11.Input: 2Output: 1Input: 1000Output: 2567605
= 24883200000Total number of digits in 24883200000 is 11.Input: 2Output: 1Input: 1000Output: 2567605
The idea of the solution is described below.
Brute force method: By brute force, we can simply compute N! in O(N) time and then multiply it n times but that will be a very slow method and would exceed both time and space because  would be a huge number.
would be a huge number.
Efficient method:
Let’s look at it more closely. We can break (N!)^N into simpler terms which are easy to compute. By taking common logarithm,
we get 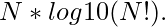
and we know, 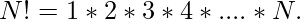
Therefore we can reduce further.
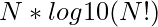
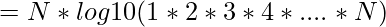
![Rendered by QuickLaTeX.com = N * [log10 (1) + log10 (2) + log10 (3) + .... + log10 (N)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ed89efe334f10a68a933e2747e5a5f11_l3.png)
Now we can compute the answer easily in O(N) time and without space limit exceeding.
So why is a valid answer to the problem?
We know that the total number of digits in a number N whose base is 10 can be easily found by taking ceil(log10 (N)). That is exactly done in the approach described above.
The code implementation of the above idea is given below.
C++
#include <bits/stdc++.h>
using namespace std;
int countDigits(int n)
{
double ans = 0;
for (int i = 1; i <= n; i++)
ans += log10(i);
ans = ans * n;
return 1 + floor(ans);
}
int main()
{
int n = 4;
cout << countDigits(n) << "\n";
return 0;
}
|
Java
import java.io.*;
class GFG
{
static int countDigits(int n)
{
double ans = 0;
for (int i = 1; i <= n; i++)
ans += Math.log10(i);
ans = ans * n;
return 1 + (int)Math.floor(ans);
}
public static void main (String[] args)
{
int n = 4;
System.out.println(
countDigits(n) + "\n");
}
}
|
Python3
import math
def countDigits( n):
ans = 0
for i in range (1,n+1):
ans += math.log10(i)
ans = ans * n
return 1 + math.floor(ans)
if __name__ == "__main__":
n = 4
print (countDigits(n))
|
C#
using System;
class GFG
{
static int countDigits(int n)
{
double ans = 0;
for (int i = 1; i <= n; i++)
ans += Math.Log10(i);
ans = ans * n;
return 1 + (int)Math.Floor(ans);
}
public static void Main ()
{
int n = 4;
Console.WriteLine(
countDigits(n) + "\n");
}
}
|
PHP
<?php
function countDigits ($n)
{
$ans = 0;
for ($i = 1; $i <= $n; $i++)
$ans += log10($i);
$ans = $ans * $n;
return 1 + floor($ans);
}
$n = 4;
echo countDigits($n) , "\n";
?>
|
Javascript
<script>
function countDigits(n)
{
let ans = 0;
for (let i = 1; i <= n; i++)
ans += Math.log10(i);
ans = ans * n;
return 1 + Math.floor(ans);
}
let n = 4;
document.write(countDigits(n) + "<br>");
</script>
|
Time complexity: O(nlogn) since calculating log in a loop
Auxiliary space: O(1) because constant variables have been used
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...