Null Space and Nullity of a Matrix

Null Space and Nullity are concepts in linear algebra which are used to identify the linear relationship among attributes.

Null Space:

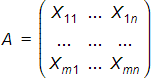
The null space of any matrix A consists of all the vectors B such that AB = 0 and B is not zero. It can also be thought as the solution obtained from AB = 0 where A is known matrix of size m x n and B is matrix to be found of size n x k. The size of the null space of the matrix provides us with the number of linear relations among attributes. 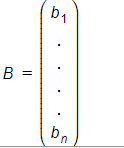A generalized description: Let a matrix be and there is one vector in the null space of A, i.e, then B satisfies the given equations, The idea –

1. AB = 0 implies every row of A when multiplied by B goes to zero. 2. Variable values in each sample(represented by a row) behave the same. 3. This helps in identifying the linear relationships in the attributes. 4. Every null space vector corresponds to one linear relationship.

Nullity:

Nullity can be defined as the number of vectors present in the null space of a given matrix. In other words, the dimension of the null space of the matrix A is called the nullity of A. The number of linear relations among the attributes is given by the size of the null space. The null space vectors B can be used to identify these linear relationship. Rank Nullity Theorem: The rank-nullity theorem helps us to relate the nullity of the data matrix to the rank and the number of attributes in the data. The rank-nullity theorem is given by –

Nullity of A + Rank of A = Total number of attributes of A (i.e. total number of columns in A)

Rank: Rank of a matrix refers to the number of linearly independent rows or columns of the matrix. Example with proof of rank-nullity theorem:

Consider the matrix A with attributes {X1, X2, X3}
    1  2  0
A = 2  4  0
    3  6  1
then,
Number of columns in A = 3

R1 and R3 are linearly independent.
The rank of the matrix A which is the 
number of non-zero rows in its echelon form are 2.
we have,
AB = 0

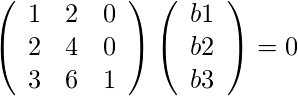Then we get,
b1 + 2*b2 = 0
b3 = 0
The null vector we can get is 

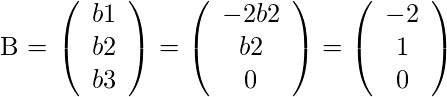The number of parameter in the general solution is the dimension 
of the null space (which is 1 in this example). Thus, the sum of 
the rank and the nullity of A  is 2 + 1 which
is equal to the number of columns of A.

This rank and nullity relationship holds true for any matrix. Python Example to find null space of a Matrix:

# Sympy is a library in python for
# symbolic Mathematics
from sympy import Matrix

# List A
A = [[1, 2, 0], [2, 4, 0], [3, 6, 1]]

# Matrix A
A = Matrix(A)

# Null Space of A
NullSpace = A.nullspace()   # Here NullSpace is a list

NullSpace = Matrix(NullSpace)   # Here NullSpace is a Matrix
print("Null Space : ", NullSpace)

# checking whether NullSpace satisfies the
# given condition or not as A * NullSpace = 0
# if NullSpace is null space of A
print(A * NullSpace)

Output:

Null Space :  Matrix([[-2], [1], [0]])
Matrix([[0], [0], [0]])

Python Example to find nullity of a Matrix:

from sympy import Matrix

A = [[1, 2, 0], [2, 4, 0], [3, 6, 1]]

A = Matrix(A)

# Number of Columns
NoC = A.shape[1]

# Rank of A
rank = A.rank()

# Nullity of the Matrix
nullity = NoC - rank

print("Nullity : ", nullity)

Output:

Nullity :  1