Nth root of a number using log

Given two integers N and K, the task is to find the N^th root of the K. 

Examples:

Input: N = 3, K = 8 
Output: 2.00 
Explanation:
Cube root of 8 is 2. i.e. 2³ = 8

Input: N = 2, K = 16 
Output: 4.00 
Explanation:
Square root of 16 is 4, i.e. 4² = 16 

Approach: The idea is to use logarithmic function to find the N^th root of K.

Let D be our N^th root of the K, 
Then,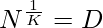 
Apply log_K on both the sides – 
=> 
=> 
=> 

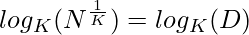
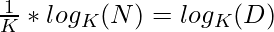
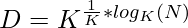
Below is the implementation of the above approach:  

C++

// C++ implementation to find the
// Kth root of a number using log

#include <bits/stdc++.h>

// Function to find the Kth root
// of the number using log function
double kthRoot(double n, int k)
{
    return pow(k,
               (1.0 / k)
                   * (log(n)
                      / log(k)));
}

// Driver Code
int main(void)
{
    double n = 81;
    int k = 4;
    printf("%lf ", kthRoot(n, k));
    return 0;
}

Java

// Java implementation to find the
// Kth root of a number using log
import java.util.*;

class GFG {

// Function to find the Kth root
// of the number using log function
static double kthRoot(double n, int k)
{
    return Math.pow(k, ((1.0 / k) *
                       (Math.log(n) /
                        Math.log(k))));
}

// Driver Code
public static void main(String args[])
{
    double n = 81;
    int k = 4;

    System.out.printf("%.6f", kthRoot(n, k));
}
}

// This code is contributed by rutvik_56

Python3

# Python3 implementation to find the
# Kth root of a number using log

import numpy as np

# Function to find the Kth root
# of the number using log function
def kthRoot(n, k):

    return pow(k, ((1.0 / k) *
                  (np.log(n) /
                   np.log(k))))

# Driver Code
n = 81
k = 4

print("%.6f" % kthRoot(n, k))

# This code is contributed by PratikBasu

C#

// C# implementation to find the
// Kth root of a number using log
using System;

class GFG {

// Function to find the Kth root
// of the number using log function
static double kthRoot(double n, int k)
{

    return Math.Pow(k, ((1.0 / k) *
                        (Math.Log(n) /
                         Math.Log(k))));
}

// Driver Code
public static void Main(String []args)
{
    double n = 81;
    int k = 4;

    Console.Write("{0:F6}", kthRoot(n, k));
}
}

// This code is contributed by AbhiThakur

Javascript

<script>

// Javascript implementation to find the
// Kth root of a number using log

// Function to find the Kth root
// of the number using log function
function kthRoot(n, k)
{
   return Math.pow(k, ((1.0 / k) *
                       (Math.log(n) /
                        Math.log(k))));
}

// Driver Code
var n = 81;
var k = 4;
var x = kthRoot(n, k)

document.write(x.toFixed(6));

// This code is contributed by Ankita saini

</script>

Output:

3.000000

Time Complexity: O(1)

Auxiliary Space: O(1)