NPDA for accepting the language L = {ambncn | m,n ≥ 1}

Prerequisite – Pushdown automata, Pushdown Automata Acceptance by Final State

Problem: Design a non deterministic PDA for accepting the language 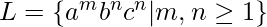, i.e.,

L = {abc, aabc, aabbcc, abbbccc, aabbbccc ...... } 

The following DFA must contain:

1. The number of a’s is equal to number of c’s.
2. The number of b’s is independent of the number of a’s and c’s.
3. Order of a, b and c must be maintained.

Explanation: The order of a’s, b’s and c’s is maintained as follows that is, all the a’s  are coming first and then all the b’s and then c’s are coming. Since the number of b’s is exactly equal to the number of c’s.So, the count of b’s and c’s will maintained by the stack. Stack used will have a start symbol and extra symbol for count of b’s and c’s.

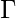 = { a, z }

Where, = set of all the stack alphabet. z = stack start symbol. 

Approach used in the construction of PDA –

• Step-1: Whenever ‘a’ comes then push it in stack and if again ‘a’ comes then also push it.
• Step-2: When ‘c’ comes then pop one ‘a’ from the stack each time.
• Step-3: When ‘b’ comes then ignore it and change the state in state diagram.
• Step-4: Stop the execution if at the end, the stack becomes empty.Thus the string is accepted by the PDA.

Note that there always maintains the order of a, b and c. 

Stack transition functions:

(q0, a, z)  (q0, z)(q0, b, z)  (q1, bz)(q1, b, b)  (q1, bb)(q1, c, b)  (q2, )(q2, c, b)  (q2, )(q2, , z)  (qf, z)

State transition diagram:

Here, q0 = Initial state qf = Final state 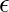= indicates pop operation And, q1,q2= Intermediate State