Normal Distribution in R
Last Updated :
13 Apr, 2020
Normal Distribution is a probability function used in statistics that tells about how the data values are distributed. It is the most important probability distribution function used in statistics because of its advantages in real case scenarios. For example, the height of the population, shoe size, IQ level, rolling a dice, and many more.
It is generally observed that data distribution is normal when there is a random collection of data from independent sources. The graph produced after plotting the value of the variable on x-axis and count of the value on y-axis is bell-shaped curve graph. The graph signifies that the peak point is the mean of the data set and half of the values of data set lie on the left side of the mean and other half lies on the right part of the mean telling about the distribution of the values. The graph is symmetric distribution.
In R, there are 4 built-in functions to generate normal distribution:
- dnorm()
dnorm(x, mean, sd)
- pnorm()
pnorm(x, mean, sd)
- qnorm()
qnorm(p, mean, sd)
- rnorm()
rnorm(n, mean, sd)
where,
– x represents the data set of values
– mean(x) represents the mean of data set x. It’s default value is 0.
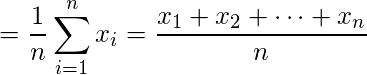
– sd(x) represents the standard deviation of data set x. It’s default value is 1.
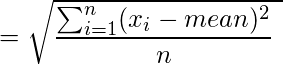
– n is the number of observations.
– p is vector of probabilities
Functions To Generate Normal Distribution in R
dnorm()
dnorm() function in R programming measures density function of distribution. In statistics, it is measured by below formula-
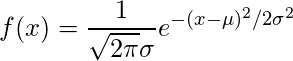
where,
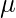
is mean and
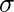
is standard deviation.
Syntax :
dnorm(x, mean, sd)
Example:
x = seq(-15, 15, by=0.1)
y = dnorm(x, mean(x), sd(x))
png(file="dnormExample.png")
plot(x, y)
dev.off()
|
Output:

pnorm()
pnorm() function is the cumulative distribution function which measures the probability that a random number X takes a value less than or equal to x i.e., in statistics it is given by-
![Rendered by QuickLaTeX.com F_X(x) = Pr[X \le x] = \alpha](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d50fb0814b23a38612a020341aa7e376_l3.png)
Syntax:
pnorm(x, mean, sd)
Example:
x <- seq(-10, 10, by=0.1)
y <- pnorm(x, mean = 2.5, sd = 2)
png(file="pnormExample.png")
plot(x, y)
dev.off()
|
Output :

qnorm()
qnorm() function is the inverse of
pnorm() function. It takes the probability value and gives output which corresponds to the probability value. It is useful in finding the percentiles of a normal distribution.
Syntax:
qnorm(p, mean, sd)
Example:
x <- seq(0, 1, by = 0.02)
y <- qnorm(x, mean(x), sd(x))
png(file = "qnormExample.png")
plot(x, y)
dev.off()
|
Output:

rnorm()
rnorm() function in R programming is used to generate a vector of random numbers which are normally distributed.
Syntax:
rnorm(x, mean, sd)
Example:
x <- rnorm(10000, mean=90, sd=5)
png(file = "rnormExample.png")
hist(x, breaks=50)
dev.off()
|
Output :

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...