Noise Models in Digital Image Processing

Last Updated : 22 Nov, 2022

The principal source of noise in digital images arises during image acquisition and transmission. The performance of imaging sensors is affected by a variety of environmental and mechanical factors of the instrument, resulting in the addition of undesirable noise in the image. Images are also corrupted during the transmission process due to non-ideal channel characteristics.

Generally, a mathematical model of image degradation and its restoration is used for processing. The figure below shows the presence of a degradation function h(x,y) and an external noise n(x,y) component coming into the original image signal f(x,y) thereby producing a final degraded image g(x,y). This part composes the degradation model. Mathematically we can write the following :

$g(x,y) = h(x,y) * f(x,y) + n(x,y)$

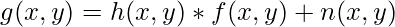
Where * indicates convolution in the spatial domain.

The goal of the restoration function or the restoration filter is to obtain a close replica F(x,y) of the original image.

The external noise is probabilistic in nature and there are several noise models used frequently in the field of digital image processing. We have several probability density functions of the noise.

Noise Models

Gaussian Noise:

Because of its mathematical simplicity, the Gaussian noise model is often used in practice and even in situations where they are marginally applicable at best. Here, m is the mean and σ² is the variance.

Gaussian noise arises in an image due to factors such as electronic circuit noise and sensor noise due to poor illumination or high temperature.

$p(z)=\frac{1}{\sigma \sqrt{2\pi }}e^{-\frac{(z-m)^{2}}{2\sigma ^{2}}}$

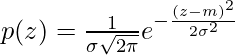
Rayleigh Noise

$p(z)=\frac{2}{b}(z-a)e^{\frac{-(z-a)^{2}}{b}} for z \ge a, and p(z) = 0 otherwise.$

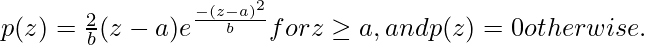
Here mean m and variance σ² are the following:

$m=a+\sqrt{\pi b/4}$

$\sigma ^{2}=\frac{b(4-\pi )}{4}$

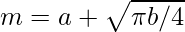
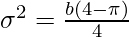
Rayleigh noise is usually used to characterize noise phenomena in range imaging.

Erlang (or gamma) Noise

$p(z)=\frac{a^{b}z^{b-1}}{(b-1)!}e^{-az} for z \ge 0 and p(z) = 0 otherwise.$

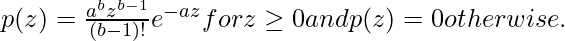
Here ! indicates factorial. The mean and variance are given below.

$m = b/a , σ2 = b/a2$

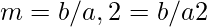
Gamma noise density finds application in laser imaging.

Exponential Noise

$p(z)=ae^{-az} for z \ge 0 and p(z) = 0 otherwise.$

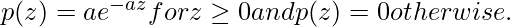
Here a > 0. The mean and variance of this noise pdf are:

$m = 1/a σ2 = 1/a2$

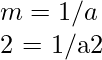
This density function is a special case of b = 1.

Exponential noise is also commonly present in cases of laser imaging.

Uniform Noise

$p(z)=\frac{1}{b-a} if a \le z \le b, and p(z) = 0 otherwise.$

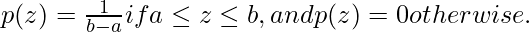
The mean and variance are given below.

$m=\frac{a+b}{2} \sigma ^{2}=\frac{(b-a)^{2}}{12}$

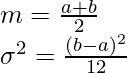
Uniform noise is not practically present but is often used in numerical simulations to analyze systems.

Impulse Noise

$p(z) = Pa for z = a, p(z) = Pb for z = b, p(z) = 0 otherwise.$

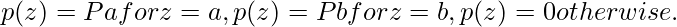
If b > a, intensity b will appear as a light dot in the image. Conversely, level a will appear like a black dot in the image. Hence, this presence of white and black dots in the image resembles to salt-and-pepper granules, hence also called salt-and-pepper noise. When either P_a or P_b is zero, it is called unipolar noise. The origin of impulse noise is quick transients such as faulty switching in cameras or other such cases.

Suggest improvement

How to Decide Window Size for a Moving Average Filter in MATLAB?

How to Apply Median Filter For RGB Image in MATLAB?

Share your thoughts in the comments

Introduction to Digital Image Processing

Image Conversion

Image Filtering Techniques

Histogram Equalization

Object Identification and Edge Detection

PhotoShop Effects in MATLAB

Image Geometry, Optical Illusion and Image Transformation

Morphologiocal Image Processing, Compression and Files

Image Coding, Comparison and Texture Features

Difference Between