NFA for language at least one of the symbols occurring an odd number of times

Problem Statement :
Design and construct Non deterministic finite automata machine that accepts the string over input alphabets (a, b, c) with atleast one of the (input symbols) have odd number of presence in the string.

Example :

aaabbbb, ababac, ababababccc ... 

Approach:

• Construct Initial state with the mark –>.
• Make transitions from one state to another on every input alphabet accordingly.
• check if there is requirement of constructing self loop or not.
• Mark final state with two concentric circles.

Designing NFA step-by-step :

Step-1:
Create an initial state “A” which transits to three different states as “B”, “C”, “D” for null.

Step-2:
On state “B” if input alphabet is ‘a’ then make transitions of ‘a’ from state “B” to “X”, and if input alphabets on state “B” are ‘b’ or ‘c’ then make self loop of ‘b’ and ‘c’ on state “B” itself.

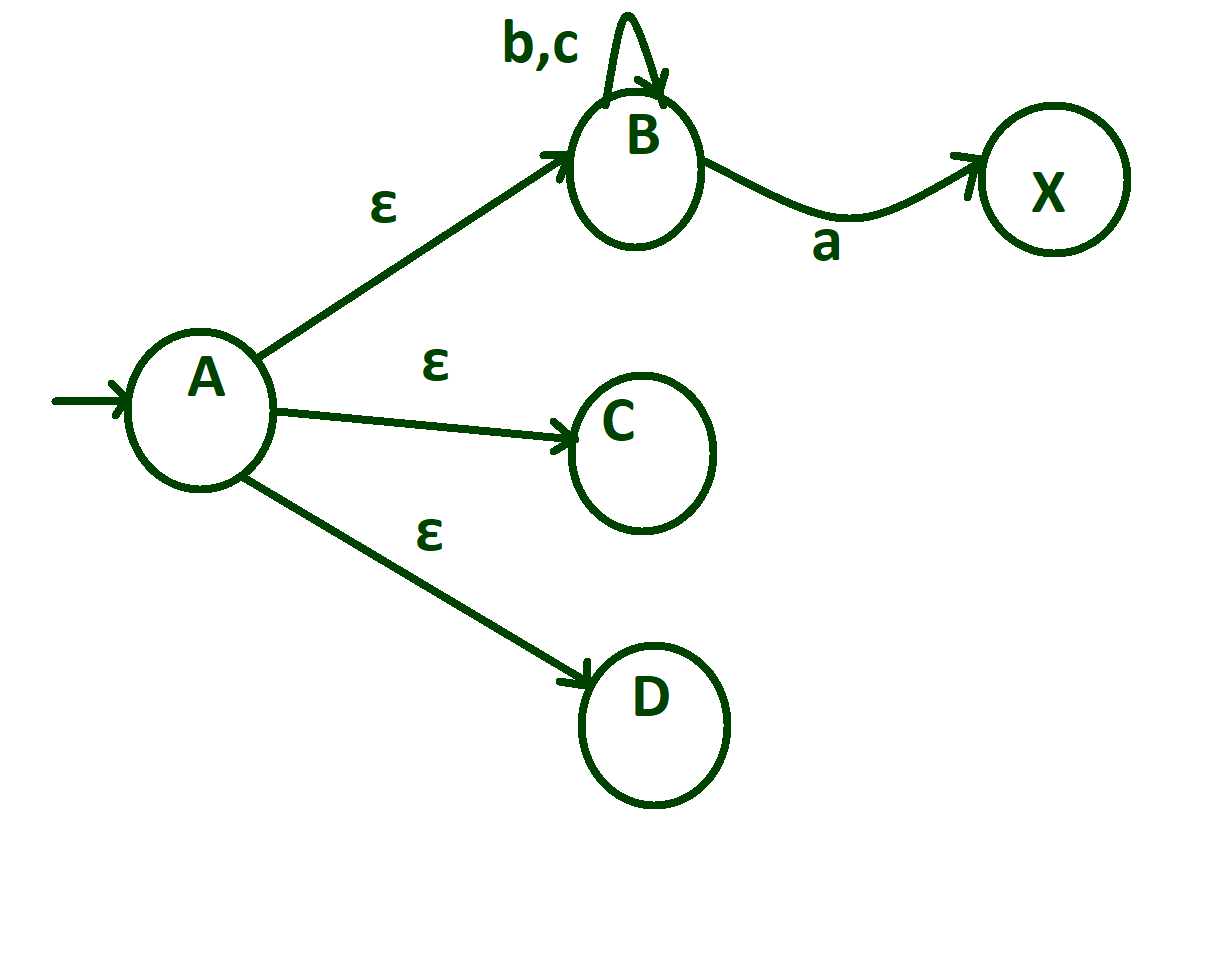
Step-3:
On state “X” input alphabets ‘b’ and ‘c’ are transits to state “X” itself but transition of ‘a’ is going from state “X” to state “B”.

Step-4:
On state “C” if input alphabet is ‘b’ then make transitions of ‘b’ from state “B” to “Y”, and if input alphabets on state “C” are ‘b’ or ‘c’ then make self-loop of ‘b’ and ‘c’ on state “C” itself And On state “Y” input alphabets ‘a’ and ‘c’ are transits to state “Y” itself but transition of ‘b’ is going from state “Y” to state “B”.

Step-5:
On state “D” if input alphabet is ‘c’ then make transitions of ‘c’ from state “D” to “Z”, and if input alphabets on state “D” are ‘b’ or ‘a’ then make self loop of ‘b’ and ‘a’ on state “D” itself. On state “Z” input alphabets ‘a’ and ‘b’ are transits to state “Z” itself but transition of ‘c’ is going from state “Z” to state “D”.

Step-6:
State “X” ensures the odd number of ‘a’, state”Y” ensures the odd number of ‘b’ and state “Z” ensures the odd number of ‘c’. So mark these here states as final states.