Nesbitt’s Inequality

Nesbitt’s inequality is one of the simplest inequalities in mathematics. According to the statement of the inequality, for any 3 given real numbers, they satisfy the mathematical condition, 
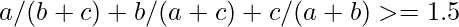for all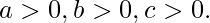 

Illustrative Examples:

The 3 numbers satisfying Nesbitts inequality are real numbers.
For a = 1, b = 2, c = 3, 
the condition of the inequality 
{1 / (2 + 3)} + {2 / (1 + 3)} + {3 / (1 + 2)} >= 1.5 holds true.

For a = 1.5, b = 5.6, c = 4.9, 
the condition of the inequality 
{1.5 / (5.6 + 4.9)} + {5.6 / (1.5 + 4.9)} + {4.9 / (1.5 + 5.6)} >= 1.5 holds true.

For a = 4, b = 6, c = 7, 
the condition of the inequality 
{4 / (6 + 7)} + {6 / (4 + 7)} + {7 / (4 + 6)} >= 1.5 holds true.

For a = 459, b = 62, c = 783, 
the condition of the inequality 
{459 / (62 + 783)} + {62 / (459 + 783)} + {783 / (459 + 62)} >= 1.5 holds true.

For a = 9, b = 6, c = 83, 
the condition of the inequality 
{9 / (6 + 83)} + {6 / (9 + 83)} + {83 / (9 + 6)} >= 1.5 holds true. 

C++

// C++ code to verify Nesbitt's Inequality
#include <bits/stdc++.h>
using namespace std;

bool isValidNesbitt(double a, double b, double c)
{
    // 3 parts of the inequality sum
    double A = a / (b + c);
    double B = b / (a + c);
    double C = c / (a + b);
    double inequality = A + B + C;

   return (inequality >= 1.5);
}

int main()
{
    double a = 1.0, b = 2.0, c = 3.0;
    if (isValidNesbitt(a, b, c))
        cout << "Nesbitt's inequality satisfied."
             << "for real numbers " << a << ", "
             << b << ", " << c << "\n";
    else
       cout << "Not satisfied";
    return 0;
}

Java

// Java code to verify Nesbitt's Inequality
class GFG {

    static boolean isValidNesbitt(double a,
                          double b, double c)
    {

        // 3 parts of the inequality sum
        double A = a / (b + c);
        double B = b / (a + c);
        double C = c / (a + b);
        double inequality = A + B + C;

        return (inequality >= 1.5);
    }

    // Driver code
    public static void main(String args[])
    {
        double a = 1.0, b = 2.0, c = 3.0;
        if(isValidNesbitt(a, b, c) == true)
        {
            System.out.print("Nesbitt's inequality"
                                  + " satisfied.");
            System.out.println("for real numbers "
                         + a + ", " + b + ", " + c);
        }
        else
            System.out.println("Nesbitts inequality"
                                + " not satisfied");
    }
}

// This code is contributed by JaideepPyne.

Python3

# Python3 code to verify
# Nesbitt's Inequality

def isValidNesbitt(a, b, c):

    # 3 parts of the
    # inequality sum
    A = a / (b + c);
    B = b / (a + c);
    C = c / (a + b);
    inequality = A + B + C;

    return (inequality >= 1.5);

# Driver Code
a = 1.0;
b = 2.0;
c = 3.0;
if (isValidNesbitt(a, b, c)):
    print("Nesbitt's inequality satisfied." ,
          " for real numbers ",a,", ",b,", ",c);
else:
    print("Not satisfied");

# This code is contributed by mits

C#

// C# code to verify
// Nesbitt's Inequality
using System;

class GFG
{
    static bool isValidNesbitt(double a,
                               double b,
                               double c)
    {

        // 3 parts of the
        // inequality sum
        double A = a / (b + c);
        double B = b / (a + c);
        double C = c / (a + b);
        double inequality = A + B + C;

        return (inequality >= 1.5);
    }

    // Driver code
    static public void Main ()
    {
    double a = 1.0, b = 2.0, c = 3.0;
    if(isValidNesbitt(a, b, c) == true)
    {
        Console.Write("Nesbitt's inequality" +
                               " satisfied ");
        Console.WriteLine("for real numbers " +
                      a + ", " + b + ", " + c);
    }
    else
        Console.WriteLine("Nesbitts inequality" +
                               " not satisfied");
    }
}

// This code is contributed by ajit

PHP

<?php
// PHP code to verify
// Nesbitt's Inequality

function isValidNesbitt($a, $b, $c)
{

    // 3 parts of the
    // inequality sum
    $A = $a / ($b + $c);
    $B = $b / ($a + $c);
    $C = $c / ($a + $b);
    $inequality = $A + $B + $C;

    return ($inequality >= 1.5);
}

    // Driver Code
    $a = 1.0;
    $b = 2.0;
    $c = 3.0;
    if (isValidNesbitt($a, $b, $c))
        echo"Nesbitt's inequality satisfied.",
            "for real numbers ", $a, ", ", $b,
                               ", ", $c, "\n";
    else
    cout <<"Not satisfied";


// This code is contributed by Ajit.
?>

Javascript

<script>

// Javascript code to verify Nesbitt's Inequality
function isValidNesbitt(a, b, c)
{

    // 3 parts of the
    // inequality sum
    let A = a / (b + c);
    let B = b / (a + c);
    let C = c / (a + b);
    let inequality = A + B + C;

    return (inequality >= 1.5);
}

// Driver code
let a = 1.0, b = 2.0, c = 3.0;
if (isValidNesbitt(a, b, c) == true)
{
    document.write("Nesbitt's inequality" +
                   " satisfied.");
    document.write("for real numbers " +
                   a + ", " + b + ", " + c);
}
else
    document.write("Nesbitts inequality" +
                   " not satisfied");

// This code is contributed by decode2207

</script>

Output :

Nesbitt's inequality satisfied.for real numbers 1, 2, 3

Time complexity : O(1) 
Auxiliary Space : O(1)