N-th polite number
Last Updated :
29 Aug, 2022
A polite number is a positive integer that can be written as the sum of two or more consecutive positive integers. Given N, find the N-th polite number.
Examples:
Input : 4
Output : 7
Explanation: The first 3 are 3(1+2), 5(2+3),
6(1+2+3).
Input : 7
Output : 11
Explanation: 3, 5, 6, 7, 9, 10, 11.
There exist an interesting pattern that only powers of 2 are not present in series of Polite numbers. Based on this fact, there exist below formula (Lambek–Moser theorem) for N-th polite number.
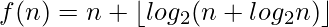
Here to find Nth polite number we have to take n as n+1 in the above equation
The inbuilt log function computes log base-e, so dividing it by log base-e 2 will give log base-2 value.
Given below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
double polite(double n)
{
n += 1;
double base = 2;
return n + (log((n + (log(n) /
log(base))))) / log(base);
}
int main()
{
double n = 7;
cout << (int)polite(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static double polite(double n)
{
n += 1;
double base = 2;
return n + (Math.log((n + (Math.log(n) /
Math.log(base))))) / Math.log(base);
}
public static void main(String[] args)
{
double n = 7;
System.out.println((int)polite(n));
}
}
|
Python
import math
def Polite(n):
n = n + 1
return (int)(n+(math.log((n + math.log(n, 2)), 2)))
n = 7
print Polite(n)
|
C#
using System;
class GFG {
static double polite(double n)
{
n += 1;
double base1 = 2;
return n + (Math.Log((n + (Math.Log(n) /
Math.Log(base1))))) /
Math.Log(base1);
}
public static void Main(String []args)
{
double n = 7;
Console.Write((int)polite(n));
}
}
|
PHP
<?php
function polite($n)
{
$n += 1;
$base = 2;
return $n + (log(($n + (log($n) /
log($base))))) / log($base);
}
$n = 7;
echo((int)polite($n));
?>
|
Javascript
<script>
function polite(n)
{
n += 1;
let base = 2;
return n + (Math.log((n + (Math.log(n) /
Math.log(base))))) / Math.log(base);
}
n = 7;
document.write(parseInt(polite(n)));
</script>
|
Output:
11
Time complexity: O(1)
Auxiliary space: O(1)
Reference: Wikipedia
Share your thoughts in the comments
Please Login to comment...