N Queen Problem using Branch And Bound

The N queens puzzle is the problem of placing N chess queens on an N×N chessboard so that no two queens threaten each other. Thus, a solution requires that no two queens share the same row, column, or diagonal.

The backtracking Algorithm for N-Queen is already discussed here. In a backtracking solution, we backtrack when we hit a dead end. In Branch and Bound solution, after building a partial solution, we figure out that there is no point going any deeper as we are going to hit a dead end. 

Let’s begin by describing the backtracking solution. “The idea is to place queens one by one in different columns, starting from the leftmost column. When we place a queen in a column, we check for clashes with already placed queens. In the current column, if we find a row for which there is no clash, we mark this row and column as part of the solution. If we do not find such a row due to clashes, then we backtrack and return false.”

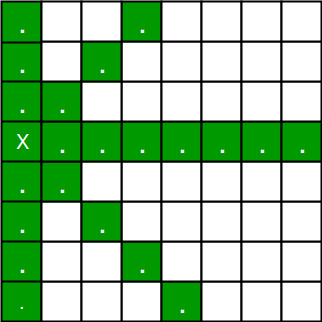
Placing 1st queen on (3, 0) and 2nd queen on (5, 1)

1. For the 1st Queen, there are total 8 possibilities as we can place 1st Queen in any row of first column. Let’s place Queen 1 on row 3.
2. After placing 1st Queen, there are 7 possibilities left for the 2nd Queen. But wait, we don’t really have 7 possibilities. We cannot place Queen 2 on rows 2, 3 or 4 as those cells are under attack from Queen 1. So, Queen 2 has only 8 – 3 = 5 valid positions left.
3. After picking a position for Queen 2, Queen 3 has even fewer options as most of the cells in its column are under attack from the first 2 Queens.

We need to figure out an efficient way of keeping track of which cells are under attack. In previous solution we kept an 8­-by­-8 Boolean matrix and update it each time we placed a queen, but that required linear time to update as we need to check for safe cells.
Basically, we have to ensure 4 things: 
1. No two queens share a column. 
2. No two queens share a row. 
3. No two queens share a top-right to left-bottom diagonal. 
4. No two queens share a top-left to bottom-right diagonal.

Number 1 is automatic because of the way we store the solution. For number 2, 3 and 4, we can perform updates in O(1) time. The idea is to keep three Boolean arrays that tell us which rows and which diagonals are occupied.

Lets do some pre-processing first. Let’s create two N x N matrix one for / diagonal and other one for \ diagonal. Let’s call them slashCode and backslashCode respectively. The trick is to fill them in such a way that two queens sharing a same /­diagonal will have the same value in matrix slashCode, and if they share same \­diagonal, they will have the same value in backslashCode matrix.
For an N x N matrix, fill slashCode and backslashCode matrix using below formula –
slashCode[row][col] = row + col 
backslashCode[row][col] = row – col + (N-1)

Using above formula will result in below matrices 

The ‘N – 1’ in the backslash code is there to ensure that the codes are never negative because we will be using the codes as indices in an array.
Now before we place queen i on row j, we first check whether row j is used (use an array to store row info). Then we check whether slash code ( j + i ) or backslash code ( j – i + 7 ) are used (keep two arrays that will tell us which diagonals are occupied). If yes, then we have to try a different location for queen i. If not, then we mark the row and the two diagonals as used and recurse on queen i + 1. After the recursive call returns and before we try another position for queen i, we need to reset the row, slash code and backslash code as unused again, like in the code from the previous notes.

Below is the implementation of above idea –  

This code Takes the Dynamic Input:

C++

#include<bits/stdc++.h>
using namespace std;
int N;


// function for printing the solution
void printSol(vector<vector<int>>board)
{
   for(int i  = 0;i<N;i++){
       for(int j = 0;j<N;j++){
           cout<<board[i][j]<<" ";
       }
       cout<<"\n";
   }
}

/*  Optimized isSafe function
isSafe function to check if current row contains or current left diagonal or current right diagonal contains any queen or not if
 yes return false
 else return true
*/

bool isSafe(int row ,int col ,vector<bool>rows , vector<bool>left_digonals ,vector<bool>Right_digonals)
{

   if(rows[row] == true || left_digonals[row+col] == true || Right_digonals[col-row+N-1] == true){
       return false;
   }

   return true;
}

// Recursive function to solve N-queen Problem
bool solve(vector<vector<int>>& board ,int col ,vector<bool>rows , vector<bool>left_digonals ,vector<bool>Right_digonals)
{
       // base Case : If all Queens are placed
       if(col>=N){
           return true;
       }

      /* Consider this Column and move  in all rows one by one */
       for(int i = 0;i<N;i++)
       {
           if(isSafe(i,col,rows,left_digonals,Right_digonals) == true)
           {
               rows[i] = true;
               left_digonals[i+col] = true;
               Right_digonals[col-i+N-1] = true;
               board[i][col] = 1;   // placing the Queen in board[i][col]

                /* recur to place rest of the queens */

               if(solve(board,col+1,rows,left_digonals,Right_digonals) == true){
                   return true;
               }

               // Backtracking
               rows[i] = false;
               left_digonals[i+col] = false;
               Right_digonals[col-i+N-1] = false;
               board[i][col] = 0;    // removing the Queen from board[i][col]

           }
       }

        return false;
}


int main()
{
   // Taking input from the user

   cout<<"Enter the no of rows for the square Board : ";
   cin>>N;


   // board of size N*N
   vector<vector<int>>board(N,vector<int>(N,0));


    // array to tell which rows are occupied
   vector<bool>rows(N,false);

   // arrays to tell which diagonals are occupied
   vector<bool>left_digonals(2*N-1,false);
   vector<bool>Right_digonals(2*N-1,false);


   bool ans =  solve(board , 0, rows,left_digonals,Right_digonals);

   if(ans == true){

       // printing the solution Board
       printSol(board);
   }
   else{
       cout<<"Solution Does not Exist\n";
   }
}
 // This Code is Contributed by Parshant Rajput

C

/* C++ program to solve N Queen Problem using Branch
   and Bound */
#include<stdio.h>
#include<string.h>
#include<stdbool.h>
#define N 8

/* A utility function to print solution */
void printSolution(int board[N][N])
{
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
            printf("%2d ", board[i][j]);
        printf("\n");
    }
}

/* A Optimized function to check if a queen can
be placed on board[row][col] */
bool isSafe(int row, int col, int slashCode[N][N],
            int backslashCode[N][N], bool rowLookup[],
      bool slashCodeLookup[], bool backslashCodeLookup[] )
{
    if (slashCodeLookup[slashCode[row][col]] ||
        backslashCodeLookup[backslashCode[row][col]] ||
        rowLookup[row])
    return false;

    return true;
}

/* A recursive utility function
to solve N Queen problem */
bool solveNQueensUtil(int board[N][N], int col,
    int slashCode[N][N], int backslashCode[N][N],
                                  bool rowLookup[N],
                            bool slashCodeLookup[],
                           bool backslashCodeLookup[] )
{
    /* base case: If all queens are placed
    then return true */
    if (col >= N)
        return true;

    /* Consider this column and try placing
       this queen in all rows one by one */
    for (int i = 0; i < N; i++)
    {
        /* Check if queen can be placed on
           board[i][col] */
        if ( isSafe(i, col, slashCode,
                    backslashCode, rowLookup,
          slashCodeLookup, backslashCodeLookup) )
        {
            /* Place this queen in board[i][col] */
            board[i][col] = 1;
            rowLookup[i] = true;
            slashCodeLookup[slashCode[i][col]] = true;
            backslashCodeLookup[backslashCode[i][col]] = true;

            /* recur to place rest of the queens */
            if ( solveNQueensUtil(board, col + 1,
                                  slashCode, backslashCode,
             rowLookup, slashCodeLookup, backslashCodeLookup) )
                return true;

            /* If placing queen in board[i][col]
            doesn't lead to a solution, then backtrack */

            /* Remove queen from board[i][col] */
            board[i][col] = 0;
            rowLookup[i] = false;
            slashCodeLookup[slashCode[i][col]] = false;
            backslashCodeLookup[backslashCode[i][col]] = false;
        }
    }

    /* If queen can not be place in any row in
        this column col then return false */
    return false;
}

/* This function solves the N Queen problem using
Branch and Bound. It mainly uses solveNQueensUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
bool solveNQueens()
{
    int board[N][N];
    memset(board, 0, sizeof board);

    // helper matrices
    int slashCode[N][N];
    int backslashCode[N][N];

    // arrays to tell us which rows are occupied
    bool rowLookup[N] = {false};

    //keep two arrays to tell us
    // which diagonals are occupied
    bool slashCodeLookup[2*N - 1] = {false};
    bool backslashCodeLookup[2*N - 1] = {false};

    // initialize helper matrices
    for (int r = 0; r < N; r++)
        for (int c = 0; c < N; c++) {
          slashCode[r] = r + c,
            backslashCode[r] = r - c + 7;
        }

    if (solveNQueensUtil(board, 0,
                          slashCode, backslashCode,
      rowLookup, slashCodeLookup, backslashCodeLookup) ==
                                                 false )
    {
        printf("Solution does not exist");
        return false;
    }

    // solution found
    printSolution(board);
    return true;
}

// Driver program to test above function
int main()
{
    solveNQueens();

    return 0;
}

Java

// Java program to solve N Queen Problem
// using Branch and Bound
import java.io.*;
import java.util.Arrays;

class GFG{

static int N = 8;

// A utility function to print solution
static void printSolution(int board[][])
{
    int N = board.length;
    for(int i = 0; i < N; i++)
    {
        for(int j = 0; j < N; j++)
            System.out.printf("%2d ", board[i][j]);

        System.out.printf("\n");
    }
}

// A Optimized function to check if a queen
// can be placed on board[row][col]
static boolean isSafe(int row, int col,
                      int slashCode[][],
                      int backslashCode[][],
                      boolean rowLookup[],
                      boolean slashCodeLookup[],
                      boolean backslashCodeLookup[])
{
    if (slashCodeLookup[slashCode[row][col]] ||
        backslashCodeLookup[backslashCode[row][col]] ||
        rowLookup[row])
        return false;

    return true;
}

// A recursive utility function to
// solve N Queen problem
static boolean solveNQueensUtil(
    int board[][], int col, int slashCode[][],
    int backslashCode[][], boolean rowLookup[],
    boolean slashCodeLookup[],
    boolean backslashCodeLookup[])
{

    // Base case: If all queens are placed
    // then return true
    int N = board.length;

    if (col >= N)
        return true;

    // Consider this column and try placing
    // this queen in all rows one by one
    for(int i = 0; i < N; i++)
    {
        // Check if queen can be placed on board[i][col]
        if (isSafe(i, col, slashCode, backslashCode,
                   rowLookup, slashCodeLookup,
                   backslashCodeLookup))
        {

            // Place this queen in board[i][col]
            board[i][col] = 1;
            rowLookup[i] = true;
            slashCodeLookup[slashCode[i][col]] = true;
            backslashCodeLookup[backslashCode[i][col]] = true;

            // recur to place rest of the queens
            if (solveNQueensUtil(
                    board, col + 1, slashCode,
                    backslashCode, rowLookup,
                    slashCodeLookup,
                    backslashCodeLookup))
                return true;

            // If placing queen in board[i][col] doesn't
            // lead to a solution, then backtrack

            // Remove queen from board[i][col]
            board[i][col] = 0;
            rowLookup[i] = false;
            slashCodeLookup[slashCode[i][col]] = false;
            backslashCodeLookup[backslashCode[i][col]] = false;
        }
    }

    // If queen can not be place in any row
    // in this column col then return false
    return false;
}

/*
 * This function solves the N Queen problem using Branch
 * and Bound. It mainly uses solveNQueensUtil() to solve
 * the problem. It returns false if queens cannot be
 * placed, otherwise return true and prints placement of
 * queens in the form of 1s. Please note that there may
 * be more than one solutions, this function prints one
 * of the feasible solutions.
 */
static boolean solveNQueens()
{
    int board[][] = new int[N][N];

    // Helper matrices
    int slashCode[][] = new int[N][N];
    int backslashCode[][] = new int[N][N];

    // Arrays to tell us which rows are occupied
    boolean[] rowLookup = new boolean[N];

    // Keep two arrays to tell us
    // which diagonals are occupied
    boolean slashCodeLookup[] = new boolean[2 * N - 1];
    boolean backslashCodeLookup[] = new boolean[2 * N - 1];

    // Initialize helper matrices
    for(int r = 0; r < N; r++)
        for(int c = 0; c < N; c++)
        {
            slashCode[r] = r + c;
            backslashCode[r] = r - c + 7;
        }

    if (solveNQueensUtil(board, 0, slashCode,
                         backslashCode, rowLookup,
                         slashCodeLookup,
                         backslashCodeLookup) == false)
    {
        System.out.printf("Solution does not exist");
        return false;
    }

    // Solution found
    printSolution(board);
    return true;
}

// Driver code
public static void main(String[] args)
{
    solveNQueens();
}
}

// This code is contributed by sujitmeshram

Python3

""" Python3 program to solve N Queen Problem
using Branch or Bound """

N = 8

""" A utility function to print solution """
def printSolution(board):
    for i in range(N):
        for j in range(N):
            print(board[i][j], end = " ")
        print()

""" A Optimized function to check if
a queen can be placed on board[row][col] """
def isSafe(row, col, slashCode, backslashCode,
           rowLookup, slashCodeLookup,
                       backslashCodeLookup):
    if (slashCodeLookup[slashCode[row][col]] or
        backslashCodeLookup[backslashCode[row][col]] or
        rowLookup[row]):
        return False
    return True

""" A recursive utility function
   to solve N Queen problem """
def solveNQueensUtil(board, col, slashCode, backslashCode,
                     rowLookup, slashCodeLookup,
                     backslashCodeLookup):

    """ base case: If all queens are
       placed then return True """
    if(col >= N):
        return True
    for i in range(N):
        if(isSafe(i, col, slashCode, backslashCode,
                  rowLookup, slashCodeLookup,
                  backslashCodeLookup)):

            """ Place this queen in board[i][col] """
            board[i][col] = 1
            rowLookup[i] = True
            slashCodeLookup[slashCode[i][col]] = True
            backslashCodeLookup[backslashCode[i][col]] = True

            """ recur to place rest of the queens """
            if(solveNQueensUtil(board, col + 1,
                                slashCode, backslashCode,
                                rowLookup, slashCodeLookup,
                                backslashCodeLookup)):
                return True

            """ If placing queen in board[i][col]
            doesn't lead to a solution,then backtrack """

            """ Remove queen from board[i][col] """
            board[i][col] = 0
            rowLookup[i] = False
            slashCodeLookup[slashCode[i][col]] = False
            backslashCodeLookup[backslashCode[i][col]] = False

    """ If queen can not be place in any row in
    this column col then return False """
    return False

""" This function solves the N Queen problem using
Branch or Bound. It mainly uses solveNQueensUtil()to
solve the problem. It returns False if queens
cannot be placed,otherwise return True or
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions,this function prints one of the
feasible solutions."""
def solveNQueens():
    board = [[0 for i in range(N)]
                for j in range(N)]

    # helper matrices
    slashCode = [[0 for i in range(N)]
                    for j in range(N)]
    backslashCode = [[0 for i in range(N)]
                        for j in range(N)]

    # arrays to tell us which rows are occupied
    rowLookup = [False] * N

    # keep two arrays to tell us
    # which diagonals are occupied
    x = 2 * N - 1
    slashCodeLookup = [False] * x
    backslashCodeLookup = [False] * x

    # initialize helper matrices
    for rr in range(N):
        for cc in range(N):
            slashCode[rr][cc] = rr + cc
            backslashCode[rr][cc] = rr - cc + 7

    if(solveNQueensUtil(board, 0, slashCode, backslashCode,
                        rowLookup, slashCodeLookup,
                        backslashCodeLookup) == False):
        print("Solution does not exist")
        return False

    # solution found
    printSolution(board)
    return True

# Driver Code
solveNQueens()

# This code is contributed by SHUBHAMSINGH10

C#

using System;
using System.Linq;

class GFG {
  static int N = 8;

  // A utility function to print solution
  static void printSolution(int[, ] board)
  {
    for (int i = 0; i < N; i++) {
      for (int j = 0; j < N; j++)
        Console.Write("{0} ", board[i, j]);

      Console.WriteLine();
    }
  }

  // A Optimized function to check if a queen
  // can be placed on board[row][col]
  static bool isSafe(int row, int col, int[, ] slashCode,
                     int[, ] backslashCode,
                     bool[] rowLookup,
                     bool[] slashCodeLookup,
                     bool[] backslashCodeLookup)
  {
    if (slashCodeLookup[slashCode[row, col]]
        || backslashCodeLookup[backslashCode[row, col]]
        || rowLookup[row])
      return false;

    return true;
  }

  // A recursive utility function to
  // solve N Queen problem
  static bool solveNQueensUtil(int[, ] board, int col,
                               int[, ] slashCode,
                               int[, ] backslashCode,
                               bool[] rowLookup,
                               bool[] slashCodeLookup,
                               bool[] backslashCodeLookup)
  {

    // Base case: If all queens are placed
    // then return true
    if (col >= N)
      return true;

    // Consider this column and try placing
    // this queen in all rows one by one
    for (int i = 0; i < N; i++) {
      // Check if queen can be placed on board[i][col]
      if (isSafe(i, col, slashCode, backslashCode,
                 rowLookup, slashCodeLookup,
                 backslashCodeLookup)) {

        // Place this queen in board[i][col]
        board[i, col] = 1;
        rowLookup[i] = true;
        slashCodeLookup[slashCode[i, col]] = true;
        backslashCodeLookup[backslashCode[i, col]]
          = true;

        // recur to place rest of the queens
        if (solveNQueensUtil(
          board, col + 1, slashCode,
          backslashCode, rowLookup,
          slashCodeLookup,
          backslashCodeLookup))
          return true;

        // If placing queen in board[i][col] doesn't
        // lead to a solution, then backtrack

        // Remove queen from board[i][col]
        board[i, col] = 0;
        rowLookup[i] = false;
        slashCodeLookup[slashCode[i, col]] = false;
        backslashCodeLookup[backslashCode[i, col]]
          = false;
      }
    }

    // If queen can not be place in any row
    // in this column col then return false
    return false;
  }

  /*
     * This function solves theN Queen problem using Branch
     * and Bound. It mainly uses solveNQueensUtil() to solve
     * the problem. It returns false if queens cannot be
     * placed, otherwise return true and prints placement of
     * queens in the form of 1s. Please note that there may
     * be more than one solutions, this function prints one
     * of the feasible solutions.
     */
  static bool solveNQueens()
  {
    int[, ] board = new int[N, N];
    // Helper matrices
    int[, ] slashCode = new int[N, N];
    int[, ] backslashCode = new int[N, N];

    // Arrays to tell us which rows are occupied
    bool[] rowLookup = new bool[N];

    // Keep two arrays to tell us
    // which diagonals are occupied
    bool[] slashCodeLookup = new bool[2 * N - 1];
    bool[] backslashCodeLookup = new bool[2 * N - 1];

    // Initialize helper arrays
    for (int r = 0; r < N; r++) {
      for (int c = 0; c < N; c++) {
        slashCode[r, c] = r + c;
        backslashCode[r, c] = r - c + N - 1;
      }
    }

    if (!solveNQueensUtil(board, 0, slashCode,
                          backslashCode, rowLookup,
                          slashCodeLookup,
                          backslashCodeLookup)) {
      Console.WriteLine("Solution does not exist");
      return false;
    }

    printSolution(board);
    return true;
  }

  // Driver code
  public static void Main() { solveNQueens(); }
}

// This code is contributed by lokeshpotta20.

Javascript

<script>

// JavaScript program to solve N Queen Problem
// using Branch and Bound

let N = 8;

// A utility function to print solution
function printSolution(board)
{
    let N = board.length;
    for(let i = 0; i < N; i++)
    {
        for(let j = 0; j < N; j++)
            document.write(board[i][j]+" ");

        document.write("<br>");
    }
}

// A Optimized function to check if a queen
// can be placed on board[row][col]
function isSafe(row,col,slashCode,backslashCode,rowLookup,slashCodeLookup,backslashCodeLookup)
{
    if (slashCodeLookup[slashCode[row][col]] ||
        backslashCodeLookup[backslashCode[row][col]] ||
        rowLookup[row])
        return false;

    return true;
}

// A recursive utility function to
// solve N Queen problem
function solveNQueensUtil(board,col,slashCode,
backslashCode,rowLookup,slashCodeLookup,backslashCodeLookup)
{
    // Base case: If all queens are placed
    // then return true
    //let N = board.length;

    if (col >= N)
        return true;

    // Consider this column and try placing
    // this queen in all rows one by one
    for(let i = 0; i < N; i++)
    {
        // Check if queen can be placed on board[i][col]
        if (isSafe(i, col, slashCode, backslashCode,
                   rowLookup, slashCodeLookup,
                   backslashCodeLookup))
        {

            // Place this queen in board[i][col]
            board[i][col] = 1;
            rowLookup[i] = true;
            slashCodeLookup[slashCode[i][col]] = true;
            backslashCodeLookup[backslashCode[i][col]] = true;

            // recur to place rest of the queens
            if (solveNQueensUtil(
                    board, col + 1, slashCode,
                    backslashCode, rowLookup,
                    slashCodeLookup,
                    backslashCodeLookup))
                return true;

            // If placing queen in board[i][col] doesn't
            // lead to a solution, then backtrack

            // Remove queen from board[i][col]
            board[i][col] = 0;
            rowLookup[i] = false;
            slashCodeLookup[slashCode[i][col]] = false;
            backslashCodeLookup[backslashCode[i][col]] = false;
        }
    }

    // If queen can not be place in any row
    // in this column col then return false
    return false;
}

/*
 * This function solves the N Queen problem using Branch
 * and Bound. It mainly uses solveNQueensUtil() to solve
 * the problem. It returns false if queens cannot be
 * placed, otherwise return true and prints placement of
 * queens in the form of 1s. Please note that there may
 * be more than one solutions, this function prints one
 * of the feasible solutions.
 */
function solveNQueens()
{
    let board = new Array(N);

    // Helper matrices
    let slashCode = new Array(N);
    let backslashCode = new Array(N);

    for(let i=0;i<N;i++)
    {
        board[i]=new Array(N);
        slashCode[i]=new Array(N);
        backslashCode[i]=new Array(N);
        for(let j=0;j<N;j++)
        {
            board[i][j]=0;
            slashCode[i][j]=0;
            backslashCode[i][j]=0;
        }
    }


    // Arrays to tell us which rows are occupied
    let rowLookup = new Array(N);
     for(let i=0;i<N;i++)
        rowLookup[i]=false;

    // Keep two arrays to tell us
    // which diagonals are occupied
    let slashCodeLookup = new Array(2 * N - 1);
    let backslashCodeLookup = new Array(2 * N - 1);
     for(let i=0;i<2*N-1;i++)
    {
        slashCodeLookup[i]=false;
        backslashCodeLookup[i]=false;
    }

    // Initialize helper matrices
    for(let r = 0; r < N; r++)
        for(let c = 0; c < N; c++)
        {
            slashCode[r] = r + c;
            backslashCode[r] = r - c + 7;
        }

    if (solveNQueensUtil(board, 0, slashCode,
                         backslashCode, rowLookup,
                         slashCodeLookup,
                         backslashCodeLookup) == false)
    {
        document.write("Solution does not exist");
        return false;
    }

    // Solution found
    printSolution(board);
    return true;
}

// Driver code
solveNQueens();


// This code is contributed by avanitrachhadiya2155

</script>

Input:

Enter the no of rows for the square Board : 8

Output :

 1  0  0  0  0  0  0  0 
 0  0  0  0  0  0  1  0 
 0  0  0  0  1  0  0  0 
 0  0  0  0  0  0  0  1 
 0  1  0  0  0  0  0  0 
 0  0  0  1  0  0  0  0 
 0  0  0  0  0  1  0  0 
 0  0  1  0  0  0  0  0

References :
https://en.wikipedia.org/wiki/Eight_queens_puzzle
www.cs.cornell.edu/~wdtseng/icpc/notes/bt2.pdf
This article is contributed by Aditya Goel. If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above