Multivariate Optimization – Gradient and Hessian
Last Updated :
24 Sep, 2021
In a multivariate optimization problem, there are multiple variables that act as decision variables in the optimization problem.
z = f(x1, x2, x3…..xn)
So, when you look at these types of problems a general function z could be some non-linear function of decision variables x1, x2, x3 to xn. So, there are n variables that one could manipulate or choose to optimize this function z. Notice that one could explain univariate optimization using pictures in two dimensions that is because in the x-direction we had the decision variable value and in the y-direction, we had the value of the function. However, if it is multivariate optimization then we have to use pictures in three dimensions and if the decision variables are more than 2 then it is difficult to visualize.
Gradient:
Before explaining gradient let us just contrast with the necessary condition of univariate case. So in case of uni-variate optimization the necessary condition for x to be the minimizer of the function f(x) is:
First-order necessary condition: f'(x) = 0
So, the derivative in a single-dimensional case becomes what we call as a gradient in the multivariate case.
According to the first-order necessary condition in univariate optimization e.g f'(x) = 0 or one can also write it as df/dx. However, since there are many variables in the case of multivariate and we have many partial derivatives and the gradient of the function f is a vector such that in each component one can compute the derivative of the function with respect to the corresponding variable. So, for example,  is the first component,
is the first component,  is the second component and
is the second component and 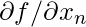 is the last component.
is the last component.
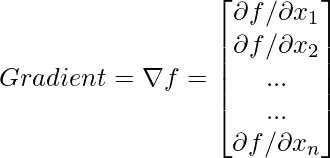
Note: Gradient of a function at a point is orthogonal to the contours.
Hessian:
Similarly in case of uni-variate optimization the sufficient condition for x to be the minimizer of the function f(x) is:
Second-order sufficiency condition: f”(x) > 0 or d2f/dx2 > 0
And this is replaced by what we call a Hessian matrix in the multivariate case. So, this is a matrix of dimension n*n, and the first component is 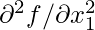 , the second component is
, the second component is  and so on.
and so on.
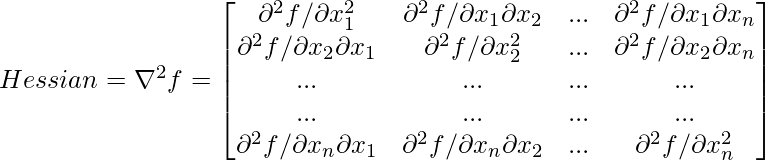
Note:
- Hessian is a symmetric matrix.
- Hessian matrix is said to be positive definite at a point if all the eigenvalues of the Hessian matrix are positive.
Share your thoughts in the comments
Please Login to comment...