This article tackles both theoretical and practical issues in Computer Science (CS). It reviews Turing Machines (TMs), a fundamental class of automata and presents a simulator for a broad variant of TMs: nondeterministic with multiple tapes. Nondeterminism is simulated by a breadth first search (BFS) of the computation tree.
The simulator is written in Python 3 and takes advantage of the power and expressiveness of this programming language, combining object oriented and functional programming techniques.
The organization is as follows. First, TMs are introduced in an informal manner, highlighting its many applications in Theoretical CS. Then, formal definitions of the basic model and the multitape variant are given. Finally, the design and implementation the simulator is presented, providing examples of its use and execution.
Introduction
TMs are abstract automata devised by Alan Turing in 1936 to investigate the limits of computation. TMs are able to compute functions following simple rules.
A TM is a primitive computational model with 3 components:
- A memory: an input-output tape divided in discrete cells that store symbols. The tape has a leftmost cell but it is unbounded to the right, so there is no limit to the length of the strings it can store.
- A control unit with a finite set of states and a tape head that points to the current cell and is able to move to the left or to the right during the computation.
- A program stored in the finite control that governs the computation of the machine.
The operation of a TM consists of three stages:
- Initialization. An input string of length N is loaded on the first N cells of the tape. The rest of infinitely many cells contain an special symbol called the blank. The machine switches to the start state.
- Computation. Each computation step involves:
- Reading the symbol in the current cell (the one being scanned by the tape head).
- Following the rules defined by the program for the combination of the current state and symbol read. The rules are called transitions or moves and consist of: (a) writing a new symbol in the current cell, (b) switching to a new state, and (c) optionally moving the head one cell to the left or to the right.
- Finalization. The computation halts when there is no rule for the current state and symbol. If the machine is in the final state, the TM accepts the input string. If the current state is nonfinal the TM rejects the input string. Note that not all TMs reach this stage because it is possible that a TM never halts on a given input, entering in an infinite loop.
TMs have many applications in Theoretical Computer Science and are strongly related to formal language theory. TMs are language recognizers that accept the top class of the Chomsky language hierarchy: the type 0 of languages generated by unrestricted grammars. They are also language transducers: given an input string of one language a TM can compute an output string of the same or a different language. This capability allows TMs to compute functions whose inputs and outputs are encoded as strings of a formal language, for example the binary numbers considered as the set of strings over the alphabet {0, 1}.
The Church-Turing states that TMs are able to compute any function that can be expressed by an algorithm. Its implications are that TMs are in fact universal computers that, being abstract mathematical devices, do not suffer from the limitations of time and space of physical ones. If this thesis is true, as many computer scientists believe, the fact discovered by Turing that there are functions that cannot be computed by a TM implies that there are functions that are not algorithmically computable by any computer past, present or future.
TMs have also been very important in the study of computational complexity and one of the central open issues in CS and mathematics: the P vs NP problem. TMs are a convenient, hardware-independent model, for analyzing the computational complexity of algorithms in terms of the number of steps performed (time complexity) or the number of cells scanned (space complexity) during the computation.
Formal definition: the basic model
A Turing Machine (TM) is a 7-tuple 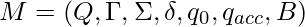 where:
where:
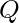 is a finite non-empty set of states.
is a finite non-empty set of states.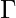 is a finite non-empty set of symbols called the tape alphabet.
is a finite non-empty set of symbols called the tape alphabet.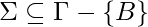 is the input alphabet.
is the input alphabet.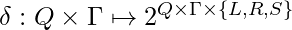 is the transition or next-move function that maps pairs of state symbol to subsets of triples state, symbol, head direction (left, right or stay).
is the transition or next-move function that maps pairs of state symbol to subsets of triples state, symbol, head direction (left, right or stay).
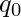 is the start state.
is the start state.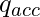 is the final accepting state.
is the final accepting state.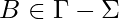 is the blank symbol.
is the blank symbol.
In each step of the computation, a TM can be described by an instantaneous description (ID). An ID is a triple 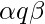 where
where 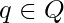 is the actual state,
is the actual state, 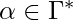 is the string contained in the cells at the left of the cell being scanned by the machine, and
is the string contained in the cells at the left of the cell being scanned by the machine, and 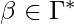 is the string contained in the current cell and the other cells to the right of the tape head until the cell that begins the infinite sequence of blanks.
is the string contained in the current cell and the other cells to the right of the tape head until the cell that begins the infinite sequence of blanks.
The binary relation 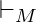 relates two IDs and is defined as follows, for all
relates two IDs and is defined as follows, for all 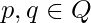 and
and 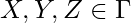 and
and 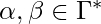 :
:
Let 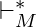 be the transitive and reflexive closure of
be the transitive and reflexive closure of 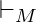 , i.e. the application of zero or more transitions between IDs. Then, the language recognized by
, i.e. the application of zero or more transitions between IDs. Then, the language recognized by 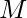 is defined as:
is defined as: 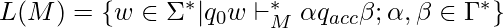 .
.
If for all states 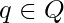 and tape symbols
and tape symbols 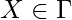 ,
, 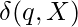 has at most one element the TM is said to be deterministic. It there exist transitions with more than one choice, the TM is nondeterministic.
has at most one element the TM is said to be deterministic. It there exist transitions with more than one choice, the TM is nondeterministic.
The sequence of IDs of deterministic TMs is linear. For nondeterministic TMs, it forms a computation tree. Nondeterminism can be thought as if the machine creates replicas of itself that proceed in parallel. This useful analogy will be used by our simulator.
At a first glance, we can think that nondeterministic TMs are more powerful than deterministic TMs because the ability to “guess” the correct path. But this is not true: a DTM is only a particular case of a NDTM, and any NDTM can be converted to a DTM. So, they have the same computational power.
In fact, several variants of TMs have been proposed: with two-way infinite tape, with several tracks, without stay option, etc. Interestingly, all of these variants are exhibit the same computational power than the basic model. They recognize the same class of languages.
In the next section we introduce a very useful variant: multitape nondeterministic TMs.
Formal definition: the multitape TM
Multitape TMs have multiple input-output tapes with independent heads. This variant does not increases the computational power of the original, but as we will see it can simplify the construction of TMs using auxiliary tapes.
A k-tape TM is a 7-tuple 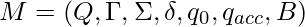 where all the elements are as in the basic TM, except the transition function that is a mapping
where all the elements are as in the basic TM, except the transition function that is a mapping 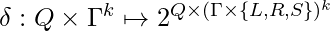 . It maps pairs of state-read symbols to subsets of pairs new states-write symbols+directions.
. It maps pairs of state-read symbols to subsets of pairs new states-write symbols+directions.
For example, the following 2-tape TM computes the sum of the numbers stored in unary notation in the first tape. The first tape contains factors: sequences of 1’s separated by 0’s that represent natural numbers. The machine writes all the 1’s in tape 2, computing the sum of all factors.
Formally, let 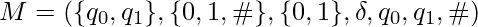 where
where 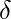 is defined as follows:
is defined as follows:
- Skip all 0’s:
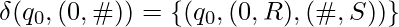
- Copy 1’s to tape 2:
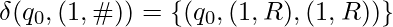
- Halt when the blank is reached:
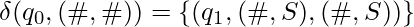
The Halting Problem
It is possible that a TM does not halt for some inputs. For example, consider the TM 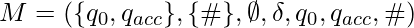 with
with 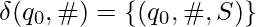 .
.
The halting problem states that it is undecidable to check if an arbitrary TM will halt on a given input string. This problem has profound implications, because it shows that there are problems that cannot be computed by TMs and, if the Church-Turing thesis is true, it means that no algorithm can solve this problems.
For a TM simulator this is very bad news, because it implies that the simulator could enter in an infinite loop.
We can not completely avoid this problem, but we can solve a restricted form of it. Consider the case of a nondeterministic TM were there are branches of the computation tree that enter an infinite loop and grow forever where others reach a final state. In this case the simulator should halt accepting the input string. But if we traverse the tree in a depth first search (DFS) fashion, the simulator will get stuck when it enters one of the infinite branches. To avoid this the simulator will traverse the computation tree via breadth first search (BFS). BFS is a graph traversal strategy that explores all the children of a branch prior to proceeding to their successors.
A simulator of multitape NDTMs in Python
In this section we will present a simulator for nondeterministic TMs with multiple tapes written in Python.
The simulator consists of two classes: a Tape class and a NDTM class.
Tape instances contain the list of current scanned cells and an index to the tape head, and provide the following operations:
- readSymbol(): returns the symbol scanned by the head, or a blank if the head is in the last scanned cell
- writeSymbol(): replaces the symbol scanned by the head by another one. If the head is in the last scanned cells, appends the symbol to the end of the list of symbols.
- moveHead(): moves the head one position to the left (-1), to the right (1) or no positions (0).
- clone(): creates a replica or copy of the tape. This will be very useful for simulating nondeterminism
NDTM instances have the following attributes:
- the start and final states.
- the current state.
- the list of tapes (Tape objects).
- a dictionary of transitions.
The transition function is implemented with a dictionary whose keys are tuples (state, read_symbols) and whose values are lists of tuples (new_state, moves). For example, the TM that adds numbers in unary notation presented before will be represented as:
{('q0', ('1', '#')): [('q0', (('1', 'R'), ('1', 'R')))],
('q0', ('0', '#')): [('q0', (('0', 'R'), ('#', 'S')))],
('q0', ('#', '#')): [('q1', (('#', 'S'), ('#', 'S')))]}
Note how the Python representation closely resembles the mathematical definition of the transition function, thanks to Python versatile data structures like dictionaries, tuples and lists. A subclass of dict, defaultdict from the standard collections module, is used to ease the burden of initialization.
NDTM objects contains methods for reading the current tuple of symbols in the tapes, for adding, getting and executing transitions and for making replicas of the current TM.
The main method of NDTM is accepts(). Its argument is an input string and it returns an NDTM object if any branch of the computation tree reaches the accepting state or None if neither branch does. It traverses the computation tree via breadth first search (BFS) to allow the computation to stop if any branch reaches the accepting state. BFS uses a queue to keep track of the pending branches. A Python deque from the collections module is used to get O(1) performance in the queue operations. The algorithm is as follows:
Add the TM instance to the queue
While queue is not empty:
Fetch the first TM from the queue
If there is no transition for the current state and read symbols:
If the TM is in a final state: return TM
Else:
If the transition is nondeterministic:
Create replicas of the TM and add them to the queue
Execute the transition in the current TM and add it to the queue
Finally, the NDTM class has methods to print the TM representation as a collection of instantaneous descriptions and to parse the TM specification from a file. As usual, this input/output facilities are the most cumbersome part of the simulator.
The specification files have the following syntax
% HEADER: mandatory
start_state final_state blank number_of_tapes
% TRANSITIONS
state read_symbols new_state write_symbol, move write_symbol, move ...
The lines starting with ‘%’ are considered comments. For example, the TM that adds numbers in unary notation has the following specification file:
% HEADER
q0 q1 # 2
% TRANSITIONS
q0 1, # q0 1, R 1, R
q0 0, # q0 0, R #, S
q0 #, # q1 #, S #, S
States and symbols can be any string not containing whitespaces or commas.
The simulator can be run from a Python session to explore the output configuration. For example if the preceding file is saved with name “2sum.tm”:
Python3
<div id="highlighter_35262" class="syntaxhighlighter nogutter "><table border="0" cellpadding="0" cellspacing="0"><tbody><tr><td class="code"><div class="container"><div class="line number1 index0 alt2"><code class="keyword">from</code> <code class="plain">NDTM </code><code class="keyword">import</code> <code class="plain">NDTM</code></div><div class="line number2 index1 alt1"><code class="plain">tm </code><code class="keyword">=</code> <code class="plain">NDTM.parse(</code><code class="string">'2sum.tm'</code><code class="plain">)</code></div><div class="line number3 index2 alt2"><code class="functions">print</code><code class="plain">(tm.accepts(</code><code class="string">'11011101'</code><code class="plain">))</code></div></div></td></tr></tbody></table></div>
|
The output shows that the simulator has produced the sum of the 1’s in tape #1:
Output :
q1: ['1', '1', '0', '1', '1', '1', '0', '1']['#']
q1: ['1', '1', '1', '1', '1', '1']['#']
The output shows the contents of the two tapes, the positions of the heads (second list of each tape) and the final state of the TM.
Source code of the simulator
Excluding input/output code and comments, the simulator is less than 100 lines of code. It is a testimony of Python power and economy. It’s object oriented but also uses functional constructs like list comprehensions.
Python3
class Tape:
def __init__(self, blank, string ='', head = 0):
self.blank = blank
self.loadString(string, head)
def loadString(self, string, head):
self.symbols = list(string)
self.head = head
def readSymbol(self):
if self.head < len(self.symbols):
return self.symbols[self.head]
else:
return self.blank
def writeSymbol(self, symbol):
if self.head < len(self.symbols):
self.symbols[self.head] = symbol
else:
self.symbols.append(symbol)
def moveHead(self, direction):
if direction == 'L': inc = -1
elif direction == 'R': inc = 1
else: inc = 0
self.head+= inc
def clone(self):
return Tape(self.blank, self.symbols, self.head)
def __str__(self):
return str(self.symbols[:self.head]) + \
str(self.symbols[self.head:])
class NDTM:
def __init__(self, start, final, blank ='#', ntapes = 1):
self.start = self.state = start
self.final = final
self.tapes = [Tape(blank) for _ in range(ntapes)]
self.trans = defaultdict(list)
def restart(self, string):
self.state = self.start
self.tapes[0].loadString(string, 0)
for tape in self.tapes[1:]:
tape.loadString('', 0)
def readSymbols(self):
return tuple(tape.readSymbol() for tape in self.tapes)
def addTrans(self, state, read_sym, new_state, moves):
self.trans[(state, read_sym)].append((new_state, moves))
def getTrans(self):
key = (self.state, self.readSymbols())
return self.trans[key] if key in self.trans else None
def execTrans(self, trans):
self.state, moves = trans
for tape, move in zip(self.tapes, moves):
symbol, direction = move
tape.writeSymbol(symbol)
tape.moveHead(direction)
return self
def clone(self):
tm = NDTM(self.start, self.final)
tm.state = self.state
tm.tapes = [tape.clone() for tape in self.tapes]
tm.trans = self.trans
return tm
def accepts(self, string):
self.restart(string)
queue = deque([self])
while len(queue) > 0:
tm = queue.popleft()
transitions = tm.getTrans()
if transitions is None:
if tm.state == tm.final: return tm
else:
for trans in transitions[1:]:
queue.append(tm.clone().execTrans(trans))
queue.append(tm.execTrans(transitions[0]))
return None
def __str__(self):
out = ''
for tape in self.tapes:
out+= self.state + ': ' + str(tape) + '\n'
return out
@staticmethod
def parse(filename):
tm = None
with open(filename) as file:
for line in file:
spec = line.strip()
if len(spec) == 0 or spec[0] == '%': continue
if tm is None:
start, final, blank, ntapes = spec.split()
ntapes = int(ntapes)
tm = NDTM(start, final, blank, ntapes)
else:
fields = line.split()
state = fields[0]
symbols = tuple(fields[1].split(', '))
new_st = fields[2]
moves = tuple(tuple(m.split(', '))
for m in fields[3:])
tm.addTrans(state, symbols, new_st, moves)
return tm
if __name__ == '__main__':
tm = NDTM('q0', 'q1', '#')
tm.addTrans('q0', ('0', ), 'q0', (('1', 'R'), ))
tm.addTrans('q0', ('1', ), 'q0', (('0', 'R'), ))
tm.addTrans('q0', ('#', ), 'q1', (('#', 'S'), ))
acc_tm = tm.accepts('11011101')
if acc_tm: print(acc_tm)
else: print('NOT ACCEPTED')
|
A nontrivial example
As a final example, we present the specification of a 3-tape TM that recognizes the non context-free language 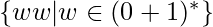 .
.
The TM nondeterministically copies the contents of the first half of the string in tape #2 and the second half in tape #3. Then, it proceeds to check if both parts match.
% 3-tape NDTM that recognizes L={ ww | w in {0, 1}* }
q0 q4 # 3
% TRANSITIONS
% put left endmarkers on tapes #2 and #3
q0 0, #, # q1 0, S $, R $, R
q0 1, #, # q1 1, S $, R $, R
% first half of string: copy symbols on tape #2
q1 0, #, # q1 0, R 0, R #, S
q1 1, #, # q1 1, R 1, R #, S
% guess second half of string: copy symbols on tape #3
q1 0, #, # q2 0, R #, S 0, R
q1 1, #, # q2 1, R #, S 1, R
q2 0, #, # q2 0, R #, S 0, R
q2 1, #, # q2 1, R #, S 1, R
% reached end of input string: switch to compare state
q2 #, #, # q3 #, S #, L #, L
% compare strings on tapes #2 and #3
q3 #, 0, 0 q3 #, S 0, L 0, L
q3 #, 1, 1 q3 #, S 1, L 1, L
% if both strings are equal switch to final state
q3 #, $, $ q4 #, S $, S $, S
Example usage. Save the above file as “3ww.tm” and run the following code:
Python3
from NDTM import NDTM
tm = NDTM.parse('3ww.tm')
print(tm.accepts('11001100'))
|
The output produced is as intended: the TM reached the final state and the contents of the two halves of the input string are in tapes #2 and #3.
Output :
q4: ['1', '1', '0', '0', '1', '1', '0', '0']['#']
q4: []['$', '1', '1', '0', '0', '#']
q4: []['$', '1', '1', '0', '0', '#']
An interesting exercise is trying to transform this TM in a one-tape nondeterministic TM or even in a one-tape deterministic one. It is perfectly possible, but the specification will be much more cumbersome. This is the utility of having multiple tapes: no more computational power but greater simplicity.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...