A Multistage graph is a directed, weighted graph in which the nodes can be divided into a set of stages such that all edges are from a stage to next stage only (In other words there is no edge between vertices of same stage and from a vertex of current stage to previous stage).
The vertices of a multistage graph are divided into n number of disjoint subsets S = { S1 , S2 , S3 ……….. Sn }, where S1 is the source and Sn is the sink ( destination ). The cardinality of S1 and Sn are equal to 1. i.e., |S1| = |Sn| = 1.
We are given a multistage graph, a source and a destination, we need to find shortest path from source to destination. By convention, we consider source at stage 1 and destination as last stage.
Following is an example graph we will consider in this article :-
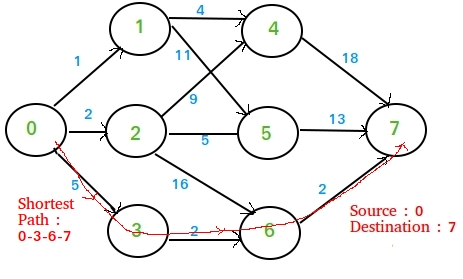
Now there are various strategies we can apply :-
- The Brute force method of finding all possible paths between Source and Destination and then finding the minimum. That’s the WORST possible strategy.
- Dijkstra’s Algorithm of Single Source shortest paths. This method will find shortest paths from source to all other nodes which is not required in this case. So it will take a lot of time and it doesn’t even use the SPECIAL feature that this MULTI-STAGE graph has.
- Simple Greedy Method – At each node, choose the shortest outgoing path. If we apply this approach to the example graph given above we get the solution as 1 + 4 + 18 = 23. But a quick look at the graph will show much shorter paths available than 23. So the greedy method fails !
- The best option is Dynamic Programming. So we need to find Optimal Sub-structure, Recursive Equations and Overlapping Sub-problems.
Optimal Substructure and Recursive Equation :-
We define the notation :- M(x, y) as the minimum cost to T(target node) from Stage x, Node y.
Shortest distance from stage 1, node 0 to
destination, i.e., 7 is M(1, 0).
// From 0, we can go to 1 or 2 or 3 to
// reach 7.
M(1, 0) = min(1 + M(2, 1),
2 + M(2, 2),
5 + M(2, 3))
This means that our problem of 0 —> 7 is now sub-divided into 3 sub-problems :-
So if we have total 'n' stages and target
as T, then the stopping condition will be :-
M(n-1, i) = i ---> T + M(n, T) = i ---> T
Recursion Tree and Overlapping Sub-Problems:-
So, the hierarchy of M(x, y) evaluations will look something like this :-
In M(i, j), i is stage number and
j is node number
M(1, 0)
/ | \
/ | \
M(2, 1) M(2, 2) M(2, 3)
/ \ / \ / \
M(3, 4) M(3, 5) M(3, 4) M(3, 5) M(3, 6) M(3, 6)
. . . . . .
. . . . . .
. . . . . .
So, here we have drawn a very small part of the Recursion Tree and we can already see Overlapping Sub-Problems. We can largely reduce the number of M(x, y) evaluations using Dynamic Programming.
Implementation details:
The below implementation assumes that nodes are numbered from 0 to N-1 from first stage (source) to last stage (destination). We also assume that the input graph is multistage.
We use top to bottom approach, and use dist[] array to store the value of overlapping sub-problem.
dist[i] will store the value of minimum distance from node i to node n-1 (target node).
Therefore, dist[0] will store minimum distance between from source node to target node.
C++
#include<bits/stdc++.h>
using namespace std;
#define N 8
#define INF INT_MAX
int shortestDist(int graph[N][N]) {
int dist[N];
dist[N-1] = 0;
for (int i = N-2 ; i >= 0 ; i--)
{
dist[i] = INF;
for (int j = i ; j < N ; j++)
{
if (graph[i][j] == INF)
continue;
dist[i] = min(dist[i], graph[i][j] +
dist[j]);
}
}
return dist[0];
}
int main()
{
int graph[N][N] =
{{INF, 1, 2, 5, INF, INF, INF, INF},
{INF, INF, INF, INF, 4, 11, INF, INF},
{INF, INF, INF, INF, 9, 5, 16, INF},
{INF, INF, INF, INF, INF, INF, 2, INF},
{INF, INF, INF, INF, INF, INF, INF, 18},
{INF, INF, INF, INF, INF, INF, INF, 13},
{INF, INF, INF, INF, INF, INF, INF, 2},
{INF, INF, INF, INF, INF, INF, INF, INF}};
cout << shortestDist(graph);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG {
static int N = 8;
static int INF = Integer.MAX_VALUE;
public static int shortestDist(int[][] graph)
{
int[] dist = new int[N];
dist[N - 1] = 0;
for (int i = N - 2; i >= 0; i--) {
dist[i] = INF;
for (int j = i; j < N; j++) {
if (graph[i][j] == INF) {
continue;
}
dist[i] = Math.min(dist[i],
graph[i][j] + dist[j]);
}
}
return dist[0];
}
public static void main(String[] args)
{
int[][] graph = new int[][] {
{ INF, 1, 2, 5, INF, INF, INF, INF },
{ INF, INF, INF, INF, 4, 11, INF, INF },
{ INF, INF, INF, INF, 9, 5, 16, INF },
{ INF, INF, INF, INF, INF, INF, 2, INF },
{ INF, INF, INF, INF, INF, INF, INF, 18 },
{ INF, INF, INF, INF, INF, INF, INF, 13 },
{ INF, INF, INF, INF, INF, INF, INF, 2 }
};
System.out.println(shortestDist(graph));
}
}
|
Python3
def shortestDist(graph):
global INF
dist = [0] * N
dist[N - 1] = 0
for i in range(N - 2, -1, -1):
dist[i] = INF
for j in range(N):
if graph[i][j] == INF:
continue
dist[i] = min(dist[i],
graph[i][j] + dist[j])
return dist[0]
N = 8
INF = 999999999999
graph = [[INF, 1, 2, 5, INF, INF, INF, INF],
[INF, INF, INF, INF, 4, 11, INF, INF],
[INF, INF, INF, INF, 9, 5, 16, INF],
[INF, INF, INF, INF, INF, INF, 2, INF],
[INF, INF, INF, INF, INF, INF, INF, 18],
[INF, INF, INF, INF, INF, INF, INF, 13],
[INF, INF, INF, INF, INF, INF, INF, 2]]
print(shortestDist(graph))
|
C#
using System;
class GFG
{
static int N = 8;
static int INF = int.MaxValue;
public static int shortestDist(int[,] graph) {
int[] dist = new int[N];
dist[N-1] = 0;
for (int i = N-2 ; i >= 0 ; i--)
{
dist[i] = INF;
for (int j = i ; j < N ; j++)
{
if (graph[i,j] == INF)
continue;
dist[i] = Math.Min(dist[i], graph[i,j] +
dist[j]);
}
}
return dist[0];
}
static void Main()
{
int[,] graph = new int[,]
{{INF, 1, 2, 5, INF, INF, INF, INF},
{INF, INF, INF, INF, 4, 11, INF, INF},
{INF, INF, INF, INF, 9, 5, 16, INF},
{INF, INF, INF, INF, INF, INF, 2, INF},
{INF, INF, INF, INF, INF, INF, INF, 18},
{INF, INF, INF, INF, INF, INF, INF, 13},
{INF, INF, INF, INF, INF, INF, INF, 2}};
Console.Write(shortestDist(graph));
}
}
|
Javascript
<script>
let N = 8;
let INF = Number.MAX_VALUE;
function shortestDist(graph)
{
let dist = new Array(N);
dist[N - 1] = 0;
for (let i = N - 2; i >= 0; i--)
{
dist[i] = INF;
for (let j = i; j < N; j++)
{
if (graph[i][j] == INF)
{
continue;
}
dist[i] = Math.min(dist[i], graph[i][j]
+ dist[j]);
}
}
return dist[0];
}
let graph = [[INF, 1, 2, 5, INF, INF, INF, INF],
[INF, INF, INF, INF, 4, 11, INF, INF],
[INF, INF, INF, INF, 9, 5, 16, INF],
[INF, INF, INF, INF, INF, INF, 2, INF],
[INF, INF, INF, INF, INF, INF, INF, 18],
[INF, INF, INF, INF, INF, INF, INF, 13],
[INF, INF, INF, INF, INF, INF, INF, 2]];
document.write(shortestDist(graph));
</script>
|
Time Complexity : The time complexity of the given code is O(N^2), where N is the number of nodes in the graph. This is because the code involves two nested loops that iterate over all pairs of nodes in the graph, and each iteration performs a constant amount of work (i.e., comparing and updating distances). Since the graph is represented using an adjacency matrix, accessing an element takes constant time. Therefore, the overall time complexity of the algorithm is O(N^2).
Space Complexity : The space complexity of the given program is O(N), where N is the number of nodes in the graph. This is because the program uses an array of size N to store the shortest distance from each node to the destination node N-1.
Algorithm
Input: A weighted multistage graph G with s and t as source and target vertices, respectively.
Output: The shortest path from s to t in G.
Set d(t) = 0 and d(v) = ? for all other vertices v in G.
For i = k-1 to 1:
a. For each vertex v in stage i:
i. Set d(v) = min(w(v, u) + d(u)) for all vertices u in stage i+1.
Return d(s) as the shortest path from s to t.
In the above algorithm, we start by setting the shortest path distance to the target vertex t as 0 and all other vertices as infinity. We then work backwards from the target vertex t to the source vertex s.
Starting from the second-to-last stage (k-1), we loop over all the vertices in that stage and update their shortest path distance based on the shortest path distances of the vertices in the next stage (i+1). We update the shortest path distance of a vertex v in stage i as the minimum of the sum of its weight w(v,u) and the shortest path distance d(u) of all vertices u in stage i+1 that are reachable from v.
After we have processed all stages and all vertices, the final shortest path distance d(s) will contain the shortest path from s to t.
Program
C++
#include <iostream>
#include <vector>
#include <unordered_map>
#include <limits>
using namespace std;
const int INF = numeric_limits<int>::max();
int multistage_shortest_path(vector<pair<int,
unordered_map<int, int>>>& graph,
int source, int target, int k) {
vector<int> d(graph.size(), INF);
d[target] = 0;
for (int i = k - 1; i > 0; i--) {
for (int v = 0; v < graph.size(); v++) {
if (graph[v].first != i) {
continue;
}
for (const auto& u : graph[v].second) {
d[v] = min(d[v], u.second + d[u.first]);
}
}
}
return d;
}
int main() {
vector<pair<int, unordered_map<int, int>>> graph = {
{0, {}},
{1, {{3, 2}, {4, 9}}},
{1, {{3, 6}, {4, 3}}},
{2, {{4, 1}}},
{2, {{5, 4}}},
{3, {{5, 7}}},
{3, {{6, 2}}},
{4, {{5, 1}, {6, 5}}},
{4, {{6, 6}}},
{5, {}},
{5, {}},
{6, {}},
{6, {}}
};
int shortest_path_distance = multistage_shortest_path(graph, 0, 12, 7);
cout << "Shortest path distance from vertex 0 to vertex 12: " <<
shortest_path_distance << endl;
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.List;
public class MultistageShortestPath {
static final int INF = Integer.MAX_VALUE;
public static int
multistageShortestPath(List<List<Pair> > graph,
int source, int target, int k)
{
int[] d = new int[graph.size()];
for (int i = 0; i < graph.size(); i++) {
d[i] = INF;
}
d[target] = 0;
for (int i = k - 1; i > 0; i--) {
for (int v = 0; v < graph.size(); v++) {
if (v != i) {
continue;
}
for (Pair u : graph.get(v)) {
d[v] = Math.min(d[v],
u.weight + d[u.vertex]);
}
}
}
return d;
}
public static void main(String[] args)
{
List<List<Pair> > graph = new ArrayList<>();
for (int i = 0; i < 12; i++) {
graph.add(new ArrayList<>());
}
graph.get(0).add(new Pair(3, 2));
graph.get(0).add(new Pair(4, 9));
graph.get(1).add(new Pair(3, 6));
graph.get(1).add(new Pair(4, 3));
graph.get(2).add(new Pair(4, 1));
graph.get(2).add(new Pair(5, 4));
graph.get(3).add(new Pair(5, 7));
graph.get(3).add(new Pair(6, 2));
graph.get(4).add(new Pair(5, 1));
graph.get(4).add(new Pair(6, 5));
graph.get(5).add(new Pair(6, 6));
int shortestPathDistance
= multistageShortestPath(graph, 0, 11, 7);
System.out.println(
"Shortest path distance from vertex 0 to vertex 11: "
+ shortestPathDistance);
}
static class Pair {
int vertex;
int weight;
public Pair(int vertex, int weight)
{
this.vertex = vertex;
this.weight = weight;
}
}
}
|
Python3
from math import inf
def multistage_shortest_path(graph, source, target, k):
d = [inf] * (len(graph))
d[target] = 0
for i in range(k-1, 0, -1):
for v in range(len(graph)):
if graph[v][0] != i:
continue
for u in graph[v][1]:
d[v] = min(d[v], graph[v][1][u] + d[u])
return d
graph = [
(0, {}),
(1, {3: 2, 4: 9}),
(1, {3: 6, 4: 3}),
(2, {4: 1}),
(2, {5: 4}),
(3, {5: 7}),
(3, {6: 2}),
(4, {5: 1, 6: 5}),
(4, {6: 6}),
(5, {}),
(5, {}),
(6, {}),
(6, {}),
]
shortest_path_distance = multistage_shortest_path(graph, 0, 12, 7)
print("Shortest path distance from vertex 0 to vertex 12:", shortest_path_distance)
|
C#
using System;
using System.Collections.Generic;
class Program
{
const int INF = int.MaxValue;
static int MultistageShortestPath(List<Tuple<int, Dictionary<int, int>>> graph, int source, int target, int k)
{
int[] d = new int[graph.Count];
for (int i = 0; i < graph.Count; i++)
d[i] = INF;
d[target] = 0;
for (int i = k - 1; i > 0; i--)
{
for (int v = 0; v < graph.Count; v++)
{
if (graph[v].Item1 != i)
continue;
foreach (var u in graph[v].Item2)
d[v] = Math.Min(d[v], u.Value + d[u.Key]);
}
}
return d;
}
static void Main(string[] args)
{
List<Tuple<int, Dictionary<int, int>>> graph = new List<Tuple<int, Dictionary<int, int>>>
{
new Tuple<int, Dictionary<int, int>>(0, new Dictionary<int, int>()),
new Tuple<int, Dictionary<int, int>>(1, new Dictionary<int, int> { { 3, 2 }, { 4, 9 } }),
new Tuple<int, Dictionary<int, int>>(1, new Dictionary<int, int> { { 3, 6 }, { 4, 3 } }),
new Tuple<int, Dictionary<int, int>>(2, new Dictionary<int, int> { { 4, 1 } }),
new Tuple<int, Dictionary<int, int>>(2, new Dictionary<int, int> { { 5, 4 } }),
new Tuple<int, Dictionary<int, int>>(3, new Dictionary<int, int> { { 5, 7 } }),
new Tuple<int, Dictionary<int, int>>(3, new Dictionary<int, int> { { 6, 2 } }),
new Tuple<int, Dictionary<int, int>>(4, new Dictionary<int, int> { { 5, 1 }, { 6, 5 } }),
new Tuple<int, Dictionary<int, int>>(4, new Dictionary<int, int> { { 6, 6 } }),
new Tuple<int, Dictionary<int, int>>(5, new Dictionary<int, int>()),
new Tuple<int, Dictionary<int, int>>(5, new Dictionary<int, int>()),
new Tuple<int, Dictionary<int, int>>(6, new Dictionary<int, int>()),
new Tuple<int, Dictionary<int, int>>(6, new Dictionary<int, int>())
};
int shortestPathDistance = MultistageShortestPath(graph, 0, 12, 7);
Console.WriteLine("Shortest path distance from vertex 0 to vertex 12: " + shortestPathDistance);
}
}
|
Javascript
function multistage_shortest_path(graph, source, target, k) {
let d = Array(graph.length).fill(Infinity);
d[target] = 0;
for (let i = k - 1; i > 0; i--) {
for (let v = 0; v < graph.length; v++) {
if (graph[v][0] != i) {
continue;
}
for (let u in graph[v][1]) {
d[v] = Math.min(d[v], graph[v][1][u] + d[u]);
}
}
}
return d;
}
let graph = [
[0, {}],
[1, {3: 2, 4: 9}],
[1, {3: 6, 4: 3}],
[2, {4: 1}],
[2, {5: 4}],
[3, {5: 7}],
[3, {6: 2}],
[4, {5: 1, 6: 5}],
[4, {6: 6}],
[5, {}],
[5, {}],
[6, {}],
[6, {}],
];
let shortest_path_distance = multistage_shortest_path(graph, 0, 12, 7);
console.log("Shortest path distance from vertex 0 to vertex 12:", shortest_path_distance);
|
Output
Shortest path distance from vertex 0 to vertex 12: inf
In the above code, the graph variable represents a multistage graph with 13 vertices and 7 stages. Each tuple in the graph list contains a vertex’s stage number and a dictionary of its adjacent vertices and their weights.
We call the multistage_shortest_path function with the graph variable, the source vertex index (0), the target vertex index (12), and the number of stages (7). The function returns the shortest path distance from the source to the target vertex, which is printed to the console.
Time and Auxiliary Space
The time complexity of the multistage graph shortest path algorithm depends on the number of vertices and the number of stages in the graph. The outer loop iterates over the stages, which takes O(k) time. The inner loop iterates over the vertices in each stage, and for each vertex, it examines its adjacent vertices. Since the graph is represented as an adjacency list, this takes O(E) time, where E is the number of edges in the graph. Therefore, the total time complexity of the algorithm is O(kE).
The space complexity of the algorithm is O(V), where V is the number of vertices in the graph. This is because we store the shortest path distances for each vertex in a list of size V. Additionally, we store the graph as an adjacency list, which also requires O(V) space.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...