Multiset Equivalence Problem
Last Updated :
23 Jun, 2022
Unlike a set, a multiset may contain multiple occurrences of same number. The multiset equivalence problem states to check if two given multisets are equal or not. For example let A = {1, 2, 3} and B = {1, 1, 2, 3}. Here A is set but B is not (1 occurs twice in B), whereas A and B are both multisets. More formally, “Are the sets of pairs defined as 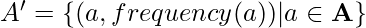 equal for the two given multisets?”
equal for the two given multisets?”
Given two multisets A and B, write a program to check if the two multisets are equal.
Note: Elements in the multisets can be of order 109
Examples:
Input : A = {1, 1, 3, 4},
B = {1, 1, 3, 4}
Output : Yes
Input : A = {1, 3},
B = {1, 1}
Output : No
Since the elements are as large as 10^9 we cannot use direct index table.
One solution is to sort both multisets and compare them one by one.
C++
#include <bits/stdc++.h>
using namespace std;
bool areSame(vector<int>& a, vector<int>& b)
{
sort(a.begin(), a.end());
sort(b.begin(), b.end());
return (a == b);
}
int main()
{
vector<int> a({ 7, 7, 5 }), b({ 7, 5, 5 });
if (areSame(a, b))
cout << "Yes\n";
else
cout << "No\n";
return 0;
}
|
Java
import java.util.*;
class GFG {
static boolean areSame(Vector<Integer>a, Vector<Integer>b)
{
Collections.sort(a);
Collections.sort(b);
return (a == b);
}
public static void main(String[] args) {
Vector<Integer> a = new Vector<Integer>(Arrays.asList( 7, 7, 5 ));
Vector<Integer> b = new Vector<Integer>(Arrays.asList( 7, 5, 5));
if (areSame(a, b))
System.out.print("Yes\n");
else
System.out.print("No\n");
}
}
|
Python3
def areSame(a, b):
a.sort();
b.sort();
return (a == b);
a = [ 7, 7, 5 ];
b = [ 7, 5, 5 ];
if (areSame(a, b)):
print("Yes");
else:
print("No");
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static bool areSame(List<int>a, List<int>b)
{
a.Sort();
b.Sort();
return (a == b);
}
public static void Main()
{
List<int> a = new List<int> { 7, 7, 5 };
List<int> b = new List<int> { 7, 5, 5 };
if (areSame(a, b))
Console.WriteLine("Yes\n");
else
Console.WriteLine("No\n");
}
}
|
Javascript
<script>
function areSame(a, b) {
a.sort((a, b) => a - b);
b.sort((a, b) => a - b);
return (a == b);
}
let a = [7, 7, 5], b = [7, 5, 5];
if (areSame(a, b))
document.write("Yes<br>");
else
document.write("No<br>");
</script>
|
Time Complexity: O(n*log(n))
Auxiliary Space: O(1)
A better solution is to use hashing. We create two empty hash tables (implemented using unordered_map in C++). We first insert all items of first multimap in first table and all items of second multiset in second table. Now we check if both hash tables contain same items and frequencies or not.
C++
#include <bits/stdc++.h>
using namespace std;
bool areSame(vector<int>& a, vector<int>& b)
{
if (a.size() != b.size())
return false;
unordered_map<int, int> m1, m2;
for (int i = 0; i < a.size(); i++) {
m1[a[i]]++;
m2[b[i]]++;
}
for (auto x : m1) {
if (m2.find(x.first) == m2.end() ||
m2[x.first] != x.second)
return false;
}
return true;
}
int main()
{
vector<int> a({ 7, 7, 5 }), b({ 7, 7, 5 });
if (areSame(a, b))
cout << "Yes\n";
else
cout << "No\n";
return 0;
}
|
Java
import java.util.*;
class GFG
{
static boolean areSame(int []a, int []b)
{
if (a.length != b.length)
return false;
HashMap<Integer, Integer> m1, m2;
m1 = new HashMap<Integer, Integer>();
m2 = new HashMap<Integer, Integer>();
for (int i = 0; i < a.length; i++)
{
if(m1.containsKey(a[i]))
{
m1.put(a[i], m1.get(a[i]) + 1);
}
else
{
m1.put(a[i], 1);
}
if(m2.containsKey(b[i]))
{
m2.put(b[i], m2.get(b[i]) + 1);
}
else
{
m2.put(b[i], 1);
}
}
for (Map.Entry<Integer, Integer> x : m1.entrySet())
{
if (!m2.containsKey(x.getKey()) ||
m2.get(x.getKey()) != x.getValue())
return false;
}
return true;
}
public static void main(String args[])
{
int []a = { 7, 7, 5 };
int []b = { 7, 7, 5 };
if (areSame(a, b))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
def areSame(a, b):
if (len(a) != len(b)):
return False
m1 = {}
m2 = {}
for i in range(len(a)):
if (a[i] in m1):
m1[a[i]] = m1[a[i]] + 1
else:
m1[a[i]] = 1
if (b[i] in m2):
m2[b[i]] = m2[b[i]] + 1
else:
m2[b[i]] = 1
for k in m1.keys():
if (k not in m1 or m2[k] != m1[k]):
return False
return True
a = [7, 7, 5]
b = [7, 7, 5]
if (areSame(a, b)):
print("Yes")
else:
print("No")
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static bool areSame(int []a, int []b)
{
if (a.Length != b.Length)
return false;
Dictionary<int, int> m1, m2;
m1 = new Dictionary<int, int>();
m2 = new Dictionary<int, int>();
for (int i = 0; i < a.Length; i++)
{
if(m1.ContainsKey(a[i]))
{
m1[a[i]] = m1[a[i]] + 1;
}
else
{
m1.Add(a[i], 1);
}
if(m2.ContainsKey(b[i]))
{
m2[b[i]] = m2[b[i]] + 1;
}
else
{
m2.Add(b[i], 1);
}
}
foreach(KeyValuePair<int, int> x in m1)
{
if (!m2.ContainsKey(x.Key) ||
m2[x.Key] != x.Value)
return false;
}
return true;
}
public static void Main(String []args)
{
int []a = { 7, 7, 5 };
int []b = { 7, 7, 5 };
if (areSame(a, b))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
function areSame(a, b)
{
if (a.length != b.length) return false;
var m1, m2;
m1 = {};
m2 = {};
for (var i = 0; i < a.length; i++)
{
if (m1.hasOwnProperty(a[i]))
{
m1[a[i]] = m1[a[i]] + 1;
} else {
m1[a[i]] = 1;
}
if (m2.hasOwnProperty(b[i])) {
m2[b[i]] = m2[b[i]] + 1;
} else {
m2[b[i]] = 1;
}
}
for (const [key, value] of Object.entries(m1)) {
if (!m2.hasOwnProperty(key) || m2[key] != value) return false;
}
return true;
}
var a = [7, 7, 5];
var b = [7, 7, 5];
if (areSame(a, b)) document.write("Yes");
else document.write("No");
</script>
|
Time complexity : O(n) under the assumption that unordered_map find() and insert() operations work in O(1) time.
Auxiliary Space: O(n)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...