Multiplication of two complex numbers given as strings

Given two complex numbers in the form of strings. Our task is to print the multiplication of these two complex numbers.

Examples:

Input : str1 = "1+1i"
        str2 = "1+1i" 
Output : "0+2i"
Here, (1 + i) * (1 + i) = 
1 + i2 + 2 * i = 2i or "0+2i"
Input : str1 = "1+-1i"
        str2 = "1+-1i"
Output : "0+-2i"
Here, (1 - i) * (1 - i) = 
1 + i2 - 2 * i = -2i or "0+-2i"

Multiplication of two complex numbers can be done as:

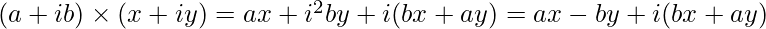
We simply split up the real and the imaginary parts of the given complex strings based on the ‘+’ and the ‘i’ symbols. We store the real parts of the two strings a and b as x[0] and y[0] respectively and the imaginary parts as x[1] and y[1] respectively. Then, we multiply the real and the imaginary parts as required after converting the extracted parts into integers. Then, we again form the return string in the required format and return the result.  

C++

// C++ Implementation of the above approach
#include <bits/stdc++.h>
using namespace std;
string complexNumberMultiply(string a, string b)
{
    int i;
    string x1;
    int temp = 1;

    // Traverse both strings, and
    // check for negative numbers
    for (i = 0; i < a.length(); i++)
    {
        if (a[i] == '+')
            break;
        if (a[i] == '-')
        {
            temp = -1;
            continue;
        }
        x1.push_back(a[i]);
    }

    // String to int
    int t1 = stoi(x1) * temp;
    x1.clear();
    temp = 1;
    for (; i < a.length() - 1; i++)
    {
        if (a[i] == '-')
        {
            temp = -1;
            continue;
        }
        x1.push_back(a[i]);
    }
    int t2 = stoi(x1) * temp;
    x1.clear();
    temp = 1;
    for (i = 0; i < b.length(); i++)
    {
        if (b[i] == '+')
            break;
        if (b[i] == '-')
        {
            temp = -1;
            continue;
        }
        x1.push_back(b[i]);
    }
    int t3 = stoi(x1) * temp;
    x1.clear();
    temp = 1;
    for (; i < b.length() - 1; i++)
    {
        if (b[i] == '-')
        {
            temp = -1;
            continue;
        }
        x1.push_back(b[i]);
    }
    int t4 = stoi(x1) * temp;

    // Real Part
    int ans = t1 * t3 - t2 * t4;
    string s;
    s += to_string(ans);
    s += '+';

    // Imaginary part
    ans = t1 * t4 + t2 * t3;
    s += to_string(ans);
    s += 'i';

    // Return the result
    return s;
}


// Driver Code
int main()
{

    string str1 = "1+1i";
    string str2 = "1+1i";
    cout << complexNumberMultiply(str1, str2);

    return 0;

    // Contributed By Bhavneet Singh
}

Java

// Java program to multiply two complex numbers
// given as strings.
import java.util.*;
import java.lang.*;

public class GfG{
    public static String complexNumberMultiply(String a, String b) {

        // Spiting the real and imaginary parts
        // of the given complex strings based on '+'
        // and 'i' symbols.
        String x[] = a.split("\\+|i");
        String y[] = b.split("\\+|i");

        // Storing the real part of complex string a
        int a_real = Integer.parseInt(x[0]);

        // Storing the imaginary part of complex string a
        int a_img = Integer.parseInt(x[1]);

        // Storing the real part of complex string b
        int b_real = Integer.parseInt(y[0]);

        // Storing the imaginary part of complex string b
        int b_img = Integer.parseInt(y[1]);

        // Returns the product.
        return (a_real * b_real - a_img * b_img) + "+" +
              (a_real * b_img + a_img * b_real) + "i";
    }

    // Driver function
    public static void main(String argc[]){
        String str1 = "1+1i";
        String str2 = "1+1i";
        System.out.println(complexNumberMultiply(str1, str2));
    }
}

Python3

# Python 3 program to multiply two complex numbers
# given as strings.
def complexNumberMultiply(a, b):

    # Spiting the real and imaginary parts
    # of the given complex strings based on '+'
    # and 'i' symbols.
    x = a.split('+')
    x[1] = x[1][:-1] # for removing 'i'

    y = b.split("+")
    y[1] = y[1][:-1] # for removing 'i'

    # Storing the real part of complex string a
    a_real = int(x[0])

    # Storing the imaginary part of complex string a
    a_img = int(x[1])


    # Storing the real part of complex string b
    b_real = int(y[0])


    # Storing the imaginary part of complex string b
    b_img = int(y[1])
    return str(a_real * b_real - a_img * b_img) \
        + "+" + str(a_real * b_img + a_img * b_real) + "i";


# Driver function

str1 = "1 + 1i"
str2 = "1 + 1i"
print(complexNumberMultiply(str1, str2))

# This code is contributed by ANKITKUMAR34

C#

// C# program to multiply two complex
// numbers given as strings.
using System;
using System.Text.RegularExpressions;

class GfG{

public static String complexNumberMultiply(String a,
                                           String b)
{

    // Spiting the real and imaginary parts
    // of the given complex strings based on '+'
    // and 'i' symbols.
    String []x = Regex.Split(a, @"\+|i");
    String []y = Regex.Split(b, @"\+|i");

    // Storing the real part of complex string a
    int a_real = Int32.Parse(x[0]);

    // Storing the imaginary part of complex string a
    int a_img = Int32.Parse(x[1]);

    // Storing the real part of complex string b
    int b_real = Int32.Parse(y[0]);

    // Storing the imaginary part of complex string b
    int b_img = Int32.Parse(y[1]);

    // Returns the product.
    return(a_real * b_real - a_img * b_img) + "+" +
          (a_real * b_img + a_img * b_real) + "i";
}

// Driver code
public static void Main(String []argc)
{
    String str1 = "1+1i";
    String str2 = "1+1i";

    Console.WriteLine(complexNumberMultiply(str1, str2));
}
}

// This code is contributed by shikhasingrajput

Javascript

<script>

// javascript program to multiply two complex numbers
// given as strings.

function complexNumberMultiply(a, b) {

    // Spiting the real and imaginary parts
    // of the given complex strings based on '+'
    // and 'i' symbols.
    var x = a.split('+');
    var y = b.split('+');

    // Storing the real part of complex string a
    var a_real = parseInt(x[0]);

    // Storing the imaginary part of complex string a
    var a_img = parseInt(x[1]);

    // Storing the real part of complex string b
    var b_real = parseInt(y[0]);

    // Storing the imaginary part of complex string b
    var b_img = parseInt(y[1]);

    // Returns the product.
    return (a_real * b_real - a_img * b_img) + "+" +
          (a_real * b_img + a_img * b_real) + "i";
}

// Driver function
var str1 = "1+1i";
var str2 = "1+1i";
document.write(complexNumberMultiply(str1, str2));

// This code contributed by shikhasingrajput
</script>

PHP

<?php
// PHP program to multiply
// two complex numbers
// given as strings.

function complexNumberMultiply($a, $b)
{

// Spiting the real and
// imaginary parts of the
// given complex strings
// based on '+' and 'i' symbols.
$x = preg_split("/[\s+]+|i/" , $a);
$y = preg_split("/[\s+]+|i/" , $b);

// Storing the real part
// of complex string a
$a_real = intval($x[0]);

// Storing the imaginary
// part of complex string a
$a_img = intval($x[1]);

// Storing the real part
// of complex string b
$b_real = intval($y[0]);

// Storing the imaginary
// part of complex string b
$b_img = intval($y[1]);

// Returns the product.
return ($a_real * $b_real -
        $a_img * $b_img) . "+" .
       ($a_real * $b_img +
        $a_img * $b_real) . "i";
}

// Driver Code
$str1 = "1+1i";
$str2 = "1+1i";
echo complexNumberMultiply($str1, $str2);

// This code is contributed by mits
?>

Output

0+2i

Time Complexity: O(len(a+b)), where len(x) is the length of strings x
Auxiliary Space: O(len(a+b)), The extras space is used to store the strings.

Approach 2: Using custom functions to parse and multiply the complex numbers

• Read the two complex numbers as strings from input.
• Parse each complex number string into its real and imaginary parts using the following steps:
  •  a. Find the position of the ‘+’ symbol in the string using the find function.
  •  Extract the real part of the complex number from the start of the string to the position of the ‘+’ symbol using the substr function and convert it to a double using the stod function.
  •  Extract the imaginary part of the complex number from the position of the ‘+’ symbol to the end of the string using the substr function and convert it to a double using the stod function. Note that the imaginary part also includes the ‘i’ symbol, which needs to be excluded from the conversion by extracting a substring from the position of the ‘+’ symbol + 1 to the position of the ‘i’ symbol – 1.
    •  Multiply the two complex numbers using the following formula:
         (a + bi) * (c + di) = (ac – bd) + (ad + bc)i
    • where a and b are the real and imaginary parts of the first complex number, and c and d are the real and imaginary parts of the second complex number.
• Print the result of the multiplication in the form a+bi, where a and b are the real and imaginary parts of the product, respectively.

C++

#include <iostream>
#include <string>

using namespace std;

struct Complex {
    double real, imag;
};

// Function to parse a string into a Complex number
Complex parse_complex(string str) {
    Complex c;

    // Get the real and imaginary parts from the string
    int pos = str.find('+');
    c.real = stod(str.substr(0, pos));
    c.imag = stod(str.substr(pos+1, str.size()-pos-2));

    return c;
}

// Function to multiply two Complex numbers
Complex multiply_complex(Complex c1, Complex c2) {
    Complex result;
    result.real = c1.real * c2.real - c1.imag * c2.imag;
    result.imag = c1.real * c2.imag + c1.imag * c2.real;
    return result;
}

int main() {
    // Input two complex numbers as strings
    string str1 = "1+1i";
    string str2 = "1+1i";

    // Parse the strings into Complex numbers
    Complex c1 = parse_complex(str1);
    Complex c2 = parse_complex(str2);

    // Multiply the Complex numbers
    Complex result = multiply_complex(c1, c2);

    // Print the result
    cout <<  result.real << "+" << result.imag << "i" << endl;

    return 0;
}

C#

using System;

namespace ComplexNumberMultiplication
{
    struct Complex
    {
        public double real;
        public double imag;
    }

    class Program
    {
        // Function to parse a string into a Complex number
        static Complex ParseComplex(string str)
        {
            Complex c;

            // Get the real and imaginary parts from the string
            int pos = str.IndexOf('+');
            c.real = double.Parse(str.Substring(0, pos));
            c.imag = double.Parse(str.Substring(pos + 1, str.Length - pos - 2));

            return c;
        }

        // Function to multiply two Complex numbers
        static Complex MultiplyComplex(Complex c1, Complex c2)
        {
            Complex result;
            result.real = c1.real * c2.real - c1.imag * c2.imag;
            result.imag = c1.real * c2.imag + c1.imag * c2.real;
            return result;
        }

        static void Main(string[] args)
        {
            // Input two complex numbers as strings
            string str1 = "1+1i";
            string str2 = "1+1i";

            // Parse the strings into Complex numbers
            Complex c1 = ParseComplex(str1);
            Complex c2 = ParseComplex(str2);

            // Multiply the Complex numbers
            Complex result = MultiplyComplex(c1, c2);

            // Print the result
            Console.WriteLine($"{result.real}+{result.imag}i");
        }
    }
}

Output

0+2i

Time complexity: O(n), where n is the length of the input strings. This is because the parse_complex function needs to parse the input strings, which has a time complexity of O(n), and the multiply_complex function performs the multiplication of the complex numbers using basic arithmetic operations, which have a time complexity of O(1).

Space complexity: O(1). This is because we only need to store the two complex numbers, the intermediate products, and the result, all of which can be stored in constant space. The only additional space used is for the Complex struct, which has a fixed size and does not depend on the length of the input strings.