MultiLabel Ranking Metrics – Ranking Loss | ML

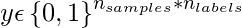
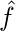
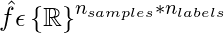
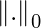
Ranking Loss is defined as the number of incorrectly ordered labels with respect to the number of correctly ordered labels. The best value of ranking loss can be zero Given a binary indicator matrix of ground-truth labels The score associated with each label is denoted by where, Ranking Loss can be calculated as : where represents number of non-zero elements in the set and represents the number of elements in the vector (cardinality of the set). The minimum ranking loss can be 0. It is when all the labels are correctly ordered in prediction labels. Code: Python code to implement Ranking Loss using the scikit-learn library.

# import sklearn and numpy libraries
import numpy as np
from sklearn.metrics import label_ranking_loss

# take sample dataset
y_true = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
y_pred_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1], [0.1, 1, 0.9]])

# calculate and print label ranking loss
print(label_ranking_loss(y_true, y_pred_score ))

# this will give minimum ranking loss
y_pred_score = np.array([[0.75, 0.5, 0.1], [0.1, 0.6, 0.1], [0.3, 0.3, 0.4]])
print(label_ranking_loss(y_true, y_pred_score ))

Output:

0.5
0

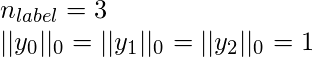
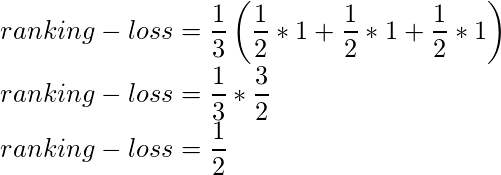
In the first sample of the first prediction, the only non-zero label has ranked in top-2 values. similarly for the second and third samples. All have only one non-label in the ground truth label. By putting these values in the formula we get, In the second print statement, All the ground truth label corresponds to the highest value in the predicted label. Hence, the ranking loss is 0. We can also got the same answer when we put those values in the formula because the rightmost term for each sample is 0. References:

• Tsoumakas, G., Katakis, I., & Vlahavas, I. (2010). Mining multi-label data. In Data mining and knowledge discovery handbook (pp. 667-685). Springer US.