Multilabel Ranking Metrics-Label Ranking Average Precision | ML
Last Updated :
23 Mar, 2020
Label Ranking average precision (LRAP) measures the average precision of the predictive model but instead using precision-recall. It measures the label rankings of each sample. Its value is always greater than
0. The best value of this metric is
1. This metric is related to average precision but used label ranking instead of precision and recall
LRAP basically asks the question that for each of the given samples what percents of the higher-ranked labels were true labels.
Given a binary indicator matrix of ground-truth labels
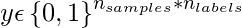 .
.
The score associated with each label is denoted by
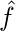
where,
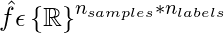
Then we can calculate LRAP using following formula:
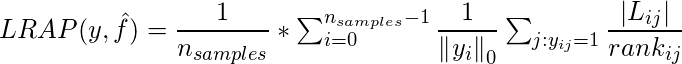
where,
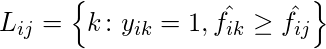
and
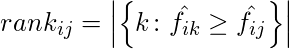 Code : Python code to implement LRAP
Code : Python code to implement LRAP
import numpy as np
from sklearn.metrics import label_ranking_average_precision_score
y_true = np.array([[1, 0, 0],
[1, 0, 1],
[1, 1, 0]])
y_score = np.array([[0.75, 0.5, 1],
[1, 0.2, 0.1],
[0.9, 0.7, 0.6]])
print(label_ranking_average_precision_score(
y_true, y_score))
|
Output :
0.777
To understand above example, Let’s take three categories human (represented by
[1, 0, 0]), cat(represented by
[0, 1, 0]), dog(represented by
[0, 0, 1]). We were provided three samples such as
[1, 0, 0], [1, 0, 1], [1, 1, 0] . This means we have total number of
5 ground truth labels (3 of humans, 1 of cat and 1 of dog). In the first sample for example, only true label human got 2
nd place in prediction label. so, rank = 2. Next we need to find out how many correct labels along the way. There is only one correct label that is human so the numerator value is 1. Hence the fraction becomes 1/2 = 0.5.
Therefore, the LRAP value of 1st sample is:
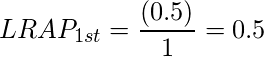
In the second sample, the first rank prediction is of human, followed by cat and dog. The fraction for the human is 1/1 = 1 and the dog is 2/3 = 0.66 (number of true label ranking along the way/ranking of dog class in the predicted label).
LRAP value of 2nd sample is:
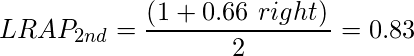
Similarly, for the third sample, the value of fractions for the human class is 1/1 = 1 and the cat class is 2/2 = 1. LRAP value of 3rd sample is:
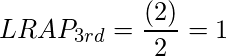
Therefore total LRAP is the sum of LRAP’s on each sample divided by the number of samples.
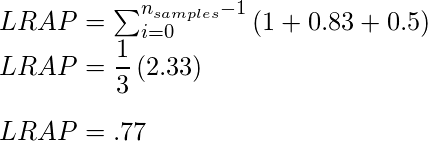
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...