MSD( Most Significant Digit ) Radix Sort
Last Updated :
26 Mar, 2024
In this article, two types of Radix Sort are discussed:
In this article, the task is to discuss the MSD Radix Sort and compare it with LSD Radix Sort.
Approach: The idea is to perform the following steps for each digit i where the value of i varies from the most significant digit to the least significant digit:
- Store elements in different buckets according to their ith digit.
- Recursively sort each bucket that has more than one element.
Most vs Least Significant Digit Radix Sort:
- The idea is to sort the fixed-length integers, MSD is more efficient than LSD because it may not have to examine every digit of each integer:
LSD Radix Sort:

MSD Radix Sort:
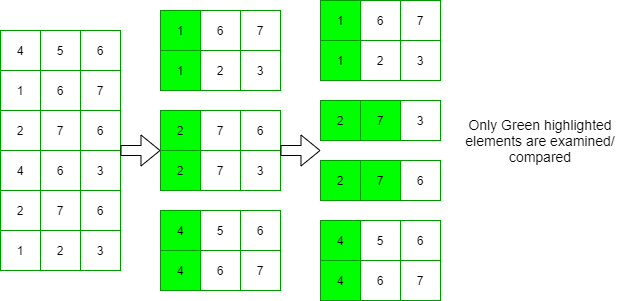
MSD Radix sort
- MSD can be used to sort strings of variable length, unlike LSD. LSD has to be stable in order to work correctly, but MSD can either be made stable or unstable and MSD can work with random strings.
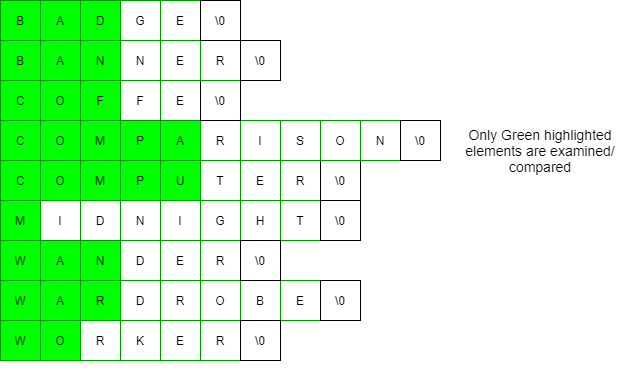
MSD Radix sort variable length string
- Time Complexity:
- Auxiliary Space:
- LSD Radix sort: O(N + B)
- MSD Radix sort: O(N + MB), where M = length of the longest string and B = size of radix (B=10 possible numbers or B=256 characters or B=2 for Binary).
- MSD uses recursion, so it requires more space than LSD. This means that MSD is much slower than LSD when working with a few inputs.
Implementation of MSD Radix Sort:
Using linked list: This implementation is for integers using linked list. A fixed-length array for every node will take a very large amount of storage.
Below is the implementation of MSD Radix Sort using a linked list:
C++
// C++ program for the implementation
// of MSD Radix Sort using linked list
#include <iostream>
#include <vector>
using namespace std;
// Linked list node structure
struct node {
vector<int> arr;
struct node* nxt[10];
};
// Function to create a new node of
// the Linked List
struct node* new_node(void)
{
struct node* tempNode = new node;
for (int i = 0; i < 10; i++) {
tempNode->nxt[i] = NULL;
}
// Return the created node
return tempNode;
}
// Function to sort the given array
// using MSD Radix Sort recursively
void msd_sort(struct node* root, int exp,
vector<int>& sorted_arr)
{
if (exp <= 0) {
return;
}
int j;
// Stores the numbers in different
// buckets according their MSD
for (int i = 0;
i < root->arr.size();
i++) {
// Get the MSD in j
j = (root->arr[i] / exp) % 10;
// If j-th index in the node
// array is empty create and
// link a new node in index
if (root->nxt[j] == NULL) {
root->nxt[j] = new_node();
}
// Store the number in j-th node
root->nxt[j]->arr.push_back(
root->arr[i]);
}
// Sort again every child node that
// has more than one number
for (int i = 0; i < 10; i++) {
// If root->next is NULL
if (root->nxt[i] != NULL) {
if (root->nxt[i]->arr.size()
> 1) {
// Sort recursively
msd_sort(root->nxt[i],
exp / 10,
sorted_arr);
}
// If any node have only
// one number then it means
// the number is sorted
else {
sorted_arr.push_back(
root->nxt[i]->arr[0]);
}
}
}
}
// Function to calculate the MSD of the
// maximum value in the array
int get_max_exp(vector<int> arr)
{
// Stores the maximum element
int mx = arr[0];
// Traverse the given array
for (int i = 1; i < arr.size(); i++) {
// Update the value of maximum
if (arr[i] > mx) {
mx = arr[i];
}
}
int exp = 1;
while (mx > 10) {
mx /= 10;
exp *= 10;
}
// Return the resultant value
return exp;
}
// Function to print an array
void print(vector<int> arr)
{
for (int i = 0; i < arr.size(); i++)
cout << arr[i] << " ";
cout << endl;
}
// Driver Code
int main()
{
// create the root node
struct node* root = new_node();
// Stores the unsorted array
// in the root node
root->arr.insert(root->arr.end(),
{ 9330, 9950, 718,
8977, 6790, 95,
9807, 741, 8586,
5710 });
cout << "Unsorted array : ";
// Print the unsorted array
print(root->arr);
// Find the optimal longest exponent
int exp = get_max_exp(root->arr);
// Stores the sorted numbers
vector<int> sorted_arr;
// Function Call
msd_sort(root, exp, sorted_arr);
cout << "Sorted array : ";
// Print the sorted array
print(sorted_arr);
return 0;
}
// C program for the implementation
// of MSD Radix Sort using linked list
// Linked list node structure
#include <stdio.h>
#include <stdlib.h> // For using malloc
#include <string.h> // For using memset
// Output array filled length
int sorted_array_length = 0;
struct node {
int arr[100];
int arr_length;
struct node* nxt[10];
};
// Function to create a new node of
// the Linked List
struct node* new_node(void)
{
struct node* tempNode
= (struct node*)malloc(sizeof(struct node));
tempNode->arr_length = 0;
for (int i = 0; i < 10; i++) {
tempNode->nxt[i] = NULL;
}
// Return the created node
return tempNode;
}
// Function to sort the given array
// using MSD Radix Sort recursively
void msd_sort(struct node* root, int exp, int* sorted_arr)
{
if (exp <= 0) {
return;
}
int j;
// Stores the numbers in different
// buckets according their MSD
for (int i = 0; i < root->arr_length; i++) {
// Get the MSD in j
j = (root->arr[i] / exp) % 10;
// If j-th index in the node
// array is empty create and
// link a new node in index
if (root->nxt[j] == NULL) {
root->nxt[j] = new_node();
}
// Store the number in j-th node
root->nxt[j]->arr[root->nxt[j]->arr_length++]
= root->arr[i];
}
// Sort again every child node that
// has more than one number
for (int i = 0; i < 10; i++) {
// If root->next is NULL
if (root->nxt[i] != NULL) {
if (root->nxt[i]->arr_length > 1) {
// Sort recursively
msd_sort(root->nxt[i], exp / 10,
sorted_arr);
}
// If any node have only
// one number then it means
// the number is sorted
else {
sorted_arr[sorted_array_length++]
= root->nxt[i]->arr[0];
}
}
}
}
// Function to calculate the MSD of the
// maximum value in the array
int get_max_exp(int* arr, int n)
{
// Stores the maximum element
int mx = arr[0];
// Traverse the given array
for (int i = 1; i < n; i++) {
// Update the value of maximum
if (arr[i] > mx) {
mx = arr[i];
}
}
int exp = 1;
while (mx > 10) {
mx /= 10;
exp *= 10;
}
// Return the resultant value
return exp;
}
// Function to print an array
void print(int* arr, int n)
{
for (int i = 0; i < n; i++)
printf("%d ", arr[i]);
printf("\n");
}
// Driver Code
int main()
{
// Unsorted array
int array[] = { 9330, 9950, 718, 8977, 6790,
95, 9807, 741, 8586, 5710 };
// Input array length
int n = sizeof(array) / sizeof(array[0]);
// create the root node
struct node* root = new_node();
// Stores the unsorted array
// in the root node and
// set arr_length
memcpy(root->arr, array, sizeof(array));
root->arr_length = n;
printf("Unsorted array : ");
// Print the unsorted array
print(root->arr, n);
// Find the optimal longest exponent
int exp = get_max_exp(root->arr, root->arr_length);
// Stores the sorted numbers
int output[n];
int* sorted_arr = &output[0];
// Function Call
msd_sort(root, exp, sorted_arr);
printf("Sorted array : ");
// Print the sorted array
print(sorted_arr, n);
return 0;
}
// Java implementation of MSD Radix Sort
// of MSD Radix Sort using counting sort()
import java.util.*;
class GFG{
// A utility function to print an array
static void print(int[] arr, int n)
{
for (int i = 0; i < n; i++) {
System.out.print(arr[i]+ " ");
}
System.out.println();
}
// A utility function to get the digit
// at index d in a integer
static int digit_at(int x, int d)
{
return (int)(x / Math.pow(10, d - 1)) % 10;
}
// The main function to sort array using
// MSD Radix Sort recursively
static int[] MSD_sort(int[] arr, int lo, int hi, int d)
{
// recursion break condition
if (hi <= lo) {
return arr;
}
int count[] = new int[10 + 2];
// temp is created to easily swap Strings in arr[]
HashMap<Integer,Integer> temp = new HashMap<>();
// Store occurrences of most significant character
// from each integer in count[]
for (int i = lo; i <= hi; i++) {
int c = digit_at(arr[i], d);
count[c + 2]++;
}
// Change count[] so that count[] now contains actual
// position of this digits in temp[]
for (int r = 0; r < 10 + 1; r++)
count[r + 1] += count[r];
// Build the temp
for (int i = lo; i <= hi; i++) {
int c = digit_at(arr[i], d);
if(temp.containsKey(count[c + 1]+1))
temp.put(count[c + 1]++, arr[i]);
else
temp.put(count[c + 1]++, arr[i]);
}
// Copy all integers of temp to arr[], so that arr[] now
// contains partially sorted integers
for (int i = lo; i <= hi; i++)
if(temp.containsKey(i-lo))
arr[i] = temp.get(i - lo);
// Recursively MSD_sort() on each partially sorted
// integers set to sort them by their next digit
for (int r = 0; r < 10; r++)
arr = MSD_sort(arr, lo + count[r], lo + count[r + 1] - 1,
d - 1);
return arr;
}
// function find the largest integer
static int getMax(int arr[], int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// Main function to call MSD_sort
static int[] radixsort(int[] arr, int n)
{
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// get the length of the largest integer
int d = (int)Math.floor(Math.log10(Math.abs(m))) + 1;
// function call
return MSD_sort(arr, 0, n - 1, d);
}
// Driver Code
public static void main(String[] args)
{
// Input array
int arr[] = { 9330, 9950, 718, 8977, 6790,
95, 9807, 741, 8586, 5710 };
// Size of the array
int n = arr.length;
System.out.printf("Unsorted array : ");
// Print the unsorted array
print(arr, n);
// Function Call
arr = radixsort(arr, n);
System.out.printf("Sorted array : ");
// Print the sorted array
print(arr, n);
}
}
// This code is contributed by gauravrajput1
// C# implementation of MSD Radix Sort
// of MSD Radix Sort using counting sort()
using System;
using System.Collections.Generic;
public class GFG {
// A utility function to print an array
static void print(int[] arr, int n) {
for (int i = 0; i < n; i++) {
Console.Write(arr[i] + " ");
}
Console.WriteLine();
}
// A utility function to get the digit
// at index d in a integer
static int digit_at(int x, int d) {
return (int) (x / Math.Pow(10, d - 1)) % 10;
}
// The main function to sort array using
// MSD Radix Sort recursively
static int[] MSD_sort(int[] arr, int lo, int hi, int d) {
// recursion break condition
if (hi <= lo) {
return arr;
}
int []count = new int[10 + 2];
// temp is created to easily swap Strings in []arr
Dictionary<int, int> temp = new Dictionary<int, int>();
// Store occurrences of most significant character
// from each integer in []count
for (int i = lo; i <= hi; i++) {
int c = digit_at(arr[i], d);
count[c + 2]++;
}
// Change []count so that []count now contains actual
// position of this digits in []temp
for (int r = 0; r < 10 + 1; r++)
count[r + 1] += count[r];
// Build the temp
for (int i = lo; i <= hi; i++) {
int c = digit_at(arr[i], d);
if (temp.ContainsKey(count[c + 1] + 1))
temp.Add(count[c + 1]++, arr[i]);
else
temp.Add(count[c + 1]++, arr[i]);
}
// Copy all integers of temp to []arr, so that []arr now
// contains partially sorted integers
for (int i = lo; i <= hi; i++)
if (temp.ContainsKey(i - lo))
arr[i] = temp[i - lo];
// Recursively MSD_sort() on each partially sorted
// integers set to sort them by their next digit
for (int r = 0; r < 10; r++)
arr = MSD_sort(arr, lo + count[r], lo + count[r + 1] - 1, d - 1);
return arr;
}
// function find the largest integer
static int getMax(int []arr, int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// Main function to call MSD_sort
static int[] radixsort(int[] arr, int n)
{
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// get the length of the largest integer
int d = (int) Math.Floor(Math.Log10(Math.Abs(m))) + 1;
// function call
return MSD_sort(arr, 0, n - 1, d);
}
// Driver Code
public static void Main(String[] args)
{
// Input array
int []arr = { 9330, 9950, 718, 8977, 6790, 95, 9807, 741, 8586, 5710 };
// Size of the array
int n = arr.Length;
Console.Write("Unsorted array : ");
// Print the unsorted array
print(arr, n);
// Function Call
arr = radixsort(arr, n);
Console.Write("Sorted array : ");
// Print the sorted array
print(arr, n);
}
}
// This code is contributed by Rajput-Ji
// javascript implementation of MSD Radix Sort
// of MSD Radix Sort using counting sort()
// A utility function to print an array
function print(arr , n) {
for (var i = 0; i < n; i++) {
document.write(arr[i] + " ");
}
document.write();
}
// A utility function to get the digit
// at index d in a integer
function digit_at(x , d) {
return parseInt( x / Math.pow(10, d - 1)) % 10;
}
// The main function to sort array using
// MSD Radix Sort recursively
function MSD_sort(arr , lo , hi , d) {
// recursion break condition
if (hi <= lo) {
return arr;
}
var count = Array(10 + 2).fill(0);
// temp is created to easily swap Strings in arr
var temp = new Map();
// Store occurrences of most significant character
// from each integer in count
for (var i = lo; i <= hi; i++) {
var c = digit_at(arr[i], d);
count[c + 2]++;
}
// Change count so that count now contains actual
// position of this digits in temp
for (var r = 0; r < 10 + 1; r++)
count[r + 1] += count[r];
// Build the temp
for (i = lo; i <= hi; i++) {
var c = digit_at(arr[i], d);
if (temp.has(count[c + 1] + 1))
temp.set(count[c + 1]++, arr[i]);
else
temp.set(count[c + 1]++, arr[i]);
}
// Copy all integers of temp to arr, so that arr now
// contains partially sorted integers
for (i = lo; i <= hi; i++)
if (temp.has(i - lo))
arr[i] = temp.get(i - lo);
// Recursively MSD_sort() on each partially sorted
// integers set to sort them by their next digit
for (r = 0; r < 10; r++)
arr = MSD_sort(arr, lo + count[r], lo + count[r + 1] - 1, d - 1);
return arr;
}
// function find the largest integer
function getMax(arr , n) {
var mx = arr[0];
for (i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// Main function to call MSD_sort
function radixsort(arr , n) {
// Find the maximum number to know number of digits
var m = getMax(arr, n);
// get the length of the largest integer
var d = parseInt( Math.floor(Math.log10(Math.abs(m)))) + 1;
// function call
return MSD_sort(arr, 0, n - 1, d);
}
// Driver Code
// Input array
var arr = [ 9330, 9950, 718, 8977, 6790, 95, 9807, 741, 8586, 5710 ];
// Size of the array
var n = arr.length;
document.write("Unsorted array : ");
// Print the unsorted array
print(arr, n);
// Function Call
arr = radixsort(arr, n);
document.write("<br/>Sorted array : ");
// Print the sorted array
print(arr, n);
// This code is contributed by Rajput-Ji
# Python implementation of MSD Radix Sort
import math
# A utility function to get the digit at index d in a integer
def digit_at(x, d):
return int(x / (10**(d-1))) % 10
# The main function to sort array using MSD Radix Sort recursively
def MSD_sort(arr, lo, hi, d):
# recursion break condition
if hi <= lo:
return arr
count = [0] * (10 + 2)
temp = [0] * (hi - lo + 1)
# Store occurrences of most significant character
# from each integer in count
for i in range(lo, hi+1):
c = digit_at(arr[i], d)
count[c + 2] += 1
# Change count so that count now contains actual
# position of this digits in temp
for r in range(10 + 1):
count[r + 1] += count[r]
# Build the temp
for i in range(lo, hi+1):
c = digit_at(arr[i], d)
temp[count[c + 1]] = arr[i]
count[c + 1] += 1
# Copy all integers of temp to arr, so that arr now
# contains partially sorted integers
for i in range(lo, hi+1):
arr[i] = temp[i - lo]
# Recursively MSD_sort() on each partially sorted
# integers set to sort them by their next digit
for r in range(10):
arr = MSD_sort(arr, lo + count[r], lo + count[r + 1] - 1, d - 1)
return arr
# function find the largest integer
def getMax(arr):
mx = arr[0]
for i in range(1, len(arr)):
if arr[i] > mx:
mx = arr[i]
return mx
# Main function to call MSD_sort
def radixsort(arr):
# Find the maximum number to know number of digits
m = getMax(arr)
# get the length of the largest integer
d = int(math.floor(math.log10(abs(m)))) + 1
# function call
return MSD_sort(arr, 0, len(arr) - 1, d)
# Driver Code
# Input array
arr = [9330, 9950, 718, 8977, 6790, 95, 9807, 741, 8586, 5710]
print("Unsorted array: ",arr)
# Function Call
arr = radixsort(arr)
print("Sorted array : ",arr)
# This code is contributed by lokeshpotta20.
OutputUnsorted array : 9330 9950 718 8977 6790 95 9807 741 8586 5710
Sorted array : 95 718 741 5710 6790 8586 8977 9330 9807 9950
Using Counting Sort() method: This implementation is for the strings based on the counting sort() method. As C style ASCII character is 1 byte. So, the 256 size array is used to count occurrences of characters, and it sorts the strings lexicographically.
Below is the implementation of MSD Radix Sort using the counting sort() method:
For string:
C++
// C++ implementation of MSD Radix Sort
#include <iostream>
#include <unordered_map>
using namespace std;
// A utility function to print an array
void print(string* str, int n)
{
for (int i = 0; i < n; i++) {
cout << str[i] << " ";
}
cout << endl;
}
// A utility function to get the ASCII value
// of the character at index d in a string
int char_at(string str, int d)
{
if (str.size() <= d)
return -1;
else
return str.at(d);
}
// The main function to sort array using
// MSD Radix Sort recursively
void MSD_sort(string* str, int lo, int hi, int d)
{
// recursion break condition
if (hi <= lo) {
return;
}
int count[256 + 2] = { 0 };
// temp is created to easily swap strings in str[]
// int temp[n] can also be used but,
// it will take more space.
unordered_map<int, string> temp;
// Store occurrences of most significant character
// from each string in count[]
for (int i = lo; i <= hi; i++) {
int c = char_at(str[i], d);
count[c + 2]++;
}
// Change count[] so that count[] now contains actual
// position of this digits in temp[]
for (int r = 0; r < 256 + 1; r++)
count[r + 1] += count[r];
// Build the temp
for (int i = lo; i <= hi; i++) {
int c = char_at(str[i], d);
temp[count[c + 1]++] = str[i];
}
// Copy all strings of temp to str[], so that str[] now
// contains partially sorted strings
for (int i = lo; i <= hi; i++)
str[i] = temp[i - lo];
// Recursively MSD_sort() on each partially sorted
// strings set to sort them by their next character
for (int r = 0; r < 256; r++)
MSD_sort(str, lo + count[r], lo + count[r + 1] - 1,
d + 1);
}
int main()
{
string str[] = { "midnight", "badge", "bag",
"worker", "banner", "wander" };
int n = sizeof(str) / sizeof(str[0]);
cout << "Unsorted array : ";
// print the unsorted array
print(str, n);
// Function call
MSD_sort(str, 0, n - 1, 0);
cout << "Sorted array : ";
// print the sorted array
print(str, n);
return 0;
}
// Java program for the above approach
import java.io.*;
import java.lang.*;
import java.util.*;
public class GFG {
// Utility function to get the ASCII
// value of the character at index d
// in the string
static int char_at(String str, int d)
{
if (str.length() <= d)
return -1;
else
return (int)(str.charAt(d));
}
// Function to sort the array using
// MSD Radix Sort recursively
static void MSD_sort(String str[], int lo, int hi,
int d)
{
// Recursive break condition
if (hi <= lo) {
return;
}
// Stores the ASCII Values
int count[] = new int[256 + 1];
// Temp is created to easily
// swap strings in str[]
HashMap<Integer, String> temp = new HashMap<>();
// Store the occurrences of the most
// significant character from
// each string in count[]
for (int i = lo; i <= hi; i++) {
int c = char_at(str[i], d);
count[c + 2]++;
}
// Change count[] so that count[]
// now contains actual position
// of this digits in temp[]
for (int r = 0; r < 256; r++)
count[r + 1] += count[r];
// Build the temp
for (int i = lo; i <= hi; i++) {
int c = char_at(str[i], d);
temp.put(count[c + 1]++, str[i]);
}
// Copy all strings of temp to str[],
// so that str[] now contains
// partially sorted strings
for (int i = lo; i <= hi; i++)
str[i] = temp.get(i - lo);
// Recursively MSD_sort() on each
// partially sorted strings set to
// sort them by their next character
for (int r = 0; r < 256; r++)
MSD_sort(str, lo + count[r],
lo + count[r + 1] - 1, d + 1);
}
// Function to print an array
static void print(String str[], int n)
{
for (int i = 0; i < n; i++) {
System.out.print(str[i] + " ");
}
System.out.println();
}
// Driver Code
public static void main(String[] args)
{
// Input String
String str[] = { "midnight", "badge", "bag",
"worker", "banner", "wander" };
// Size of the string
int n = str.length;
System.out.print("Unsorted array : ");
// Print the unsorted array
print(str, n);
// Function Call
MSD_sort(str, 0, n - 1, 0);
System.out.print("Sorted array : ");
// Print the sorted array
print(str, n);
}
}
// This code is contributed by Kingash.
// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG{
// Utility function to get the ASCII
// value of the character at index d
// in the string
static int char_at(String str, int d)
{
if (str.Length <= d)
return -1;
else
return(int)(str[d]);
}
// Function to sort the array using
// MSD Radix Sort recursively
static void MSD_sort(String []str, int lo,
int hi, int d)
{
// Recursive break condition
if (hi <= lo)
{
return;
}
// Stores the ASCII Values
int []count = new int[256 + 1];
// Temp is created to easily
// swap strings in []str
Dictionary<int,
String> temp = new Dictionary<int,
String>();
// Store the occurrences of the most
// significant character from
// each string in []count
for(int i = lo; i <= hi; i++)
{
int c = char_at(str[i], d);
count[c + 2]++;
}
// Change []count so that []count
// now contains actual position
// of this digits in []temp
for(int r = 0; r < 256; r++)
count[r + 1] += count[r];
// Build the temp
for(int i = lo; i <= hi; i++)
{
int c = char_at(str[i], d);
temp.Add(count[c + 1]++, str[i]);
}
// Copy all strings of temp to []str,
// so that []str now contains
// partially sorted strings
for(int i = lo; i <= hi; i++)
str[i] = temp[i - lo];
// Recursively MSD_sort() on each
// partially sorted strings set to
// sort them by their next character
for(int r = 0; r < 256; r++)
MSD_sort(str, lo + count[r],
lo + count[r + 1] - 1,
d + 1);
}
// Function to print an array
static void print(String []str, int n)
{
for(int i = 0; i < n; i++)
{
Console.Write(str[i] + " ");
}
Console.WriteLine();
}
// Driver Code
public static void Main(String[] args)
{
// Input String
String []str = { "midnight", "badge", "bag",
"worker", "banner", "wander" };
// Size of the string
int n = str.Length;
Console.Write("Unsorted array : ");
// Print the unsorted array
print(str, n);
// Function Call
MSD_sort(str, 0, n - 1, 0);
Console.Write("Sorted array : ");
// Print the sorted array
print(str, n);
}
}
// This code is contributed by shikhasingrajput
// JS implementation of MSD Radix Sort
// A utility function to print an array
function print(str, n)
{
for (let i = 0; i < n; i++) {
console.log(str[i] + " ");
}
console.log("<br>");
}
// A utility function to get the ASCII value
// of the character at index d in a string
function char_at( str, d)
{
if (str.length <= d)
return -1;
else
return str.charCodeAt(d);
}
// The main function to sort array using
// MSD Radix Sort recursively
function MSD_sort( str, lo, hi, d)
{
// recursion break condition
if (hi <= lo) {
return;
}
let count = new Array(256 + 2).fill(0);
// temp is created to easily swap strings in str[]
// int temp[n] can also be used but,
// it will take more space.
let temp = new Map();
// Store occurrences of most significant character
// from each string in count[]
for (let i = lo; i <= hi; i++) {
let c = char_at(str[i], d);
count[c + 2]++;
}
// Change count[] so that count[] now contains actual
// position of this digits in temp[]
for (let r = 0; r < 256 + 1; r++)
count[r + 1] += count[r];
// Build the temp
for (let i = lo; i <= hi; i++) {
let c = char_at(str[i], d);
temp.set(count[c + 1]++,str[i]);
}
// Copy all strings of temp to str[], so that str[] now
// contains partially sorted strings
for (let i = lo; i <= hi; i++)
str[i] = temp.get(i - lo);
// Recursively MSD_sort() on each partially sorted
// strings set to sort them by their next character
for (let r = 0; r < 256; r++)
MSD_sort(str, lo + count[r], lo + count[r + 1] - 1,
d + 1);
}
let str = [ "midnight", "badge", "bag", "worker", "banner", "wander" ];
let n = str.length;
console.log("Unsorted array : ");
// print the unsorted array
print(str, n);
// Function call
MSD_sort(str, 0, n - 1, 0);
console.log("Sorted array : ");
// print the sorted array
print(str, n);
import collections
# Utility function to get the ASCII value of the character at index d in the string
def char_at(string, d):
if len(string) <= d:
return -1
else:
return ord(string[d])
# Function to sort the array using MSD Radix Sort recursively
def MSD_sort(string_list, lo, hi, d):
# Recursive break condition
if hi <= lo:
return
# Stores the ASCII Values
count = [0] * (256 + 1)
# Temp is created to easily swap strings in str[]
temp = collections.defaultdict(str)
# Store the occurrences of the most significant character from each string in count[]
for i in range(lo, hi+1):
c = char_at(string_list[i], d)
count[c + 2] += 1
# Change count[] so that count[] now contains actual position of this digits in temp[]
for r in range(256):
count[r + 1] += count[r]
# Build the temp
for i in range(lo, hi+1):
c = char_at(string_list[i], d)
temp[count[c + 1]] = string_list[i]
count[c + 1] += 1
# Copy all strings of temp to str[], so that str[] now contains partially sorted strings
for i in range(lo, hi+1):
string_list[i] = temp[i - lo]
# Recursively MSD_sort() on each partially sorted strings set to sort them by their next character
for r in range(256):
MSD_sort(string_list, lo + count[r], lo + count[r + 1] - 1, d + 1)
# Function to print an array
def print_list(string_list):
for i in string_list:
print(i, end=" ")
print()
# Driver Code
if __name__ == '__main__':
# Input String
string_list = ["midnight", "badge", "bag", "worker", "banner", "wander"]
# Size of the string
n = len(string_list)
print("Unsorted array : ", end="")
# Print the unsorted array
print_list(string_list)
# Function Call
MSD_sort(string_list, 0, n - 1, 0)
print("Sorted array : ", end="")
# Print the sorted array
print_list(string_list)
OutputUnsorted array : midnight badge bag worker banner wander
Sorted array : badge bag banner midnight wander worker
For Integer:
C++
// C++ implementation of MSD Radix Sort
// of MSD Radix Sort using counting sort()
#include <iostream>
#include <math.h>
#include <unordered_map>
using namespace std;
// A utility function to print an array
void print(int* arr, int n)
{
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
// A utility function to get the digit
// at index d in a integer
int digit_at(int x, int d)
{
return (int)(x / pow(10, d - 1)) % 10;
}
// The main function to sort array using
// MSD Radix Sort recursively
void MSD_sort(int* arr, int lo, int hi, int d)
{
// recursion break condition
if (hi <= lo) {
return;
}
int count[10 + 2] = { 0 };
// temp is created to easily swap strings in arr[]
unordered_map<int, int> temp;
// Store occurrences of most significant character
// from each integer in count[]
for (int i = lo; i <= hi; i++) {
int c = digit_at(arr[i], d);
count[c + 2]++;
}
// Change count[] so that count[] now contains actual
// position of this digits in temp[]
for (int r = 0; r < 10 + 1; r++)
count[r + 1] += count[r];
// Build the temp
for (int i = lo; i <= hi; i++) {
int c = digit_at(arr[i], d);
temp[count[c + 1]++] = arr[i];
}
// Copy all integers of temp to arr[], so that arr[] now
// contains partially sorted integers
for (int i = lo; i <= hi; i++)
arr[i] = temp[i - lo];
// Recursively MSD_sort() on each partially sorted
// integers set to sort them by their next digit
for (int r = 0; r < 10; r++)
MSD_sort(arr, lo + count[r], lo + count[r + 1] - 1,
d - 1);
}
// function find the largest integer
int getMax(int arr[], int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// Main function to call MSD_sort
void radixsort(int* arr, int n)
{
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// get the length of the largest integer
int d = floor(log10(abs(m))) + 1;
// function call
MSD_sort(arr, 0, n - 1, d);
}
// Driver Code
int main()
{
// Input array
int arr[] = { 9330, 9950, 718, 8977, 6790,
95, 9807, 741, 8586, 5710 };
// Size of the array
int n = sizeof(arr) / sizeof(arr[0]);
printf("Unsorted array : ");
// Print the unsorted array
print(arr, n);
// Function Call
radixsort(arr, n);
printf("Sorted array : ");
// Print the sorted array
print(arr, n);
return 0;
}
// Java implementation of MSD Radix Sort
// of MSD Radix Sort using counting sort()
import java.util.*;
class GFG{
// A utility function to print an array
static void print(int[] arr, int n)
{
for (int i = 0; i < n; i++) {
System.out.print(arr[i]+ " ");
}
System.out.println();
}
// A utility function to get the digit
// at index d in a integer
static int digit_at(int x, int d)
{
return (int)(x / Math.pow(10, d - 1)) % 10;
}
// The main function to sort array using
// MSD Radix Sort recursively
static void MSD_sort(int[] arr, int lo, int hi, int d)
{
// recursion break condition
if (hi <= lo) {
return;
}
int count[] = new int[10 + 2];
// temp is created to easily swap Strings in arr[]
HashMap<Integer,Integer> temp = new HashMap<>();
// Store occurrences of most significant character
// from each integer in count[]
for (int i = lo; i <= hi; i++) {
int c = digit_at(arr[i], d);
count[c + 2]++;
}
// Change count[] so that count[] now contains actual
// position of this digits in temp[]
for (int r = 0; r < 10 + 1; r++)
count[r + 1] += count[r];
// Build the temp
for (int i = lo; i <= hi; i++) {
int c = digit_at(arr[i], d);
temp.put(count[c + 1]++, arr[i]);
}
// Copy all integers of temp to arr[], so that arr[] now
// contains partially sorted integers
for (int i = lo; i <= hi; i++)
arr[i] = temp.get(i - lo);
// Recursively MSD_sort() on each partially sorted
// integers set to sort them by their next digit
for (int r = 0; r < 10; r++)
MSD_sort(arr, lo + count[r], lo + count[r + 1] - 1,
d - 1);
}
// function find the largest integer
static int getMax(int arr[], int n)
{
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// Main function to call MSD_sort
static void radixsort(int[] arr, int n)
{
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// get the length of the largest integer
int d = (int)Math.floor(Math.log10(Math.abs(m))) + 1;
// function call
MSD_sort(arr, 0, n - 1, d);
}
// Driver Code
public static void main(String[] args)
{
// Input array
int arr[] = { 9330, 9950, 718, 8977, 6790,
95, 9807, 741, 8586, 5710 };
// Size of the array
int n = arr.length;
System.out.printf("Unsorted array : ");
// Print the unsorted array
print(arr, n);
// Function Call
radixsort(arr, n);
System.out.printf("Sorted array : ");
// Print the sorted array
print(arr, n);
}
}
// This code is contributed by Rajput-Ji
# A utility function to print an array
def print_array(arr):
for num in arr:
print num,
# A utility function to get the digit at index d in an integer
def digit_at(x, d):
return (x // (10 ** (d - 1))) % 10
# The main function to sort array using MSD Radix Sort recursively
def MSD_sort(arr, lo, hi, d):
# Recursion break condition
if hi <= lo:
return
count = [0] * (10 + 2)
temp = {}
# Store occurrences of most significant character from each integer in count[]
for i in range(lo, hi + 1):
c = digit_at(arr[i], d)
count[c + 2] += 1
# Change count[] so that count[] now contains actual position of these digits in temp[]
for r in range(10 + 1):
count[r + 1] += count[r]
# Build the temp
for i in range(lo, hi + 1):
c = digit_at(arr[i], d)
temp[count[c + 1]] = arr[i]
count[c + 1] += 1
# Copy all integers of temp to arr[], so that arr[] now contains partially sorted integers
for i in range(lo, hi + 1):
arr[i] = temp.get(i - lo + 1, 0)
# Recursively MSD_sort() on each partially sorted integers set to sort them by their next digit
for r in range(10):
MSD_sort(arr, lo + count[r], lo + count[r + 1] - 1, d - 1)
# Function to find the largest integer
def getMax(arr):
mx = arr[0]
for num in arr:
if num > mx:
mx = num
return mx
# Main function to call MSD_sort
def radixsort(arr):
# Find the maximum number to know the number of digits
m = getMax(arr)
# Get the length of the largest integer
d = len(str(abs(m)))
# Function call
MSD_sort(arr, 0, len(arr) - 1, d)
# Driver Code
if __name__ == "__main__":
# Input array
arr = [9330, 9950, 718, 8977, 6790, 95, 9807, 741, 8586, 5710]
print "Unsorted array:",
print_array(arr)
# Function Call
radixsort(arr)
print "Sorted array:",
print_array(arr)
// C# implementation of MSD Radix Sort
// of MSD Radix Sort using counting sort()
using System;
using System.Collections.Generic;
public class GFG {
// A utility function to print an array
static void print(int[] arr, int n) {
for (int i = 0; i < n; i++) {
Console.Write(arr[i] + " ");
}
Console.WriteLine();
}
// A utility function to get the digit
// at index d in a integer
static int digit_at(int x, int d) {
return (int) (x / Math.Pow(10, d - 1)) % 10;
}
// The main function to sort array using
// MSD Radix Sort recursively
static void MSD_sort(int[] arr, int lo, int hi, int d) {
// recursion break condition
if (hi <= lo) {
return;
}
int []count = new int[10 + 2];
// temp is created to easily swap Strings in []arr
Dictionary<int, int> temp = new Dictionary<int, int>();
// Store occurrences of most significant character
// from each integer in []count
for (int i = lo; i <= hi; i++) {
int c = digit_at(arr[i], d);
count[c + 2]++;
}
// Change []count so that []count now contains actual
// position of this digits in []temp
for (int r = 0; r < 10 + 1; r++)
count[r + 1] += count[r];
// Build the temp
for (int i = lo; i <= hi; i++) {
int c = digit_at(arr[i], d);
temp.Add(count[c + 1]++, arr[i]);
}
// Copy all integers of temp to []arr, so that []arr now
// contains partially sorted integers
for (int i = lo; i <= hi; i++)
arr[i] = temp[i - lo];
// Recursively MSD_sort() on each partially sorted
// integers set to sort them by their next digit
for (int r = 0; r < 10; r++)
MSD_sort(arr, lo + count[r], lo + count[r + 1] - 1, d - 1);
}
// function find the largest integer
static int getMax(int []arr, int n) {
int mx = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
// Main function to call MSD_sort
static void radixsort(int[] arr, int n)
{
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// get the length of the largest integer
int d = (int) Math.Floor(Math.Log10(Math.Abs(m))) + 1;
// function call
MSD_sort(arr, 0, n - 1, d);
}
// Driver Code
public static void Main(String[] args)
{
// Input array
int []arr = { 9330, 9950, 718, 8977, 6790, 95, 9807, 741, 8586, 5710 };
// Size of the array
int n = arr.Length;
Console.Write("Unsorted array : ");
// Print the unsorted array
print(arr, n);
// Function Call
radixsort(arr, n);
Console.Write("Sorted array : ");
// Print the sorted array
print(arr, n);
}
}
// This code is contributed by Rajput-Ji
// JS implementation of MSD Radix Sort
// of MSD Radix Sort using counting sort()
function print(arr, n) {
console.log(arr.join(" "))
}
function digit_at(x, d) {
return Math.floor(x / Math.pow(10, d - 1)) % 10;
}
function MSD_sort(arr, lo, hi, d) {
// recursion break condition
if (hi <= lo) {
return;
}
let count = new Array(10 + 2).fill(0);
// temp is created to easily swap Strings in []arr
let temp = {};
// Store occurrences of most significant character
// from each integer in []count
for (let i = lo; i <= hi; i++) {
let c = digit_at(arr[i], d);
count[c + 2]++;
}
// Change []count so that []count now contains actual
// position of this digits in []temp
for (let r = 0; r < 10 + 1; r++)
count[r + 1] += count[r];
// Build the temp
for (let i = lo; i <= hi; i++) {
let c = digit_at(arr[i], d);
temp[count[c + 1]++] = arr[i];
}
// Copy all integers of temp to []arr, so that []arr now
// contains partially sorted integers
for (let i = lo; i <= hi; i++)
arr[i] = temp[i - lo];
// Recursively MSD_sort() on each partially sorted
// integers set to sort them by their next digit
for (let r = 0; r < 10; r++)
MSD_sort(arr, lo + count[r], lo + count[r + 1] - 1, d - 1);
}
function getMax(arr, n) {
let mx = arr[0];
for (let i = 1; i < n; i++)
if (arr[i] > mx)
mx = arr[i];
return mx;
}
function radixsort(arr, n) {
// Find the maximum number to know number of digits
let m = getMax(arr, n);
// get the length of the largest integer
let d = Math.floor(Math.log10(Math.abs(m))) + 1;
// function call
MSD_sort(arr, 0, n - 1, d);
}
// Driver Code
let arr = [9330, 9950, 718, 8977, 6790, 95, 9807, 741, 8586, 5710];
// Size of the array
let n = arr.length;
console.log("Unsorted array : ");
// Print the unsorted array
print(arr, n);
// Function Call
radixsort(arr, n);
console.log("Sorted array : ");
// Print the sorted array
print(arr, n);
// This code is contributed by phasing17
OutputUnsorted array : 9330 9950 718 8977 6790 95 9807 741 8586 5710
Sorted array : 95 718 741 5710 6790 8586 8977 9330 9807 9950
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...