Motion of Center of Mass
Last Updated :
13 Aug, 2021
Center of Mass is an important property of any rigid body system. Usually, these systems contain more than one particle. It becomes essential to analyze these systems as a whole. To perform calculations of mechanics, these bodies must be considered as a single point mass. The Center of mass denotes such a point. Often the mechanical systems move in a transitory or a rotatory manner. In that case, the Center of mass also moves and acquires some velocity and acceleration. Let’s see how to calculate these metrics for such systems in detail.
Center of Mass
A lot of problems can be simplified if it is assumed that the mass of the object is located at one particular point. If the correct position is chosen, then equations of forces and motion behave the same way as they behave if applied when mass is spread out. This special location is termed the Center of Mass.
Its position is defined relative to an object or the system of objects whose Center of mass is to be calculated. Usually for uniform shapes, it’s their centroid. For the shapes that are symmetrical and uniform, their Center of mass is located at their centroid. For a ring, its Center of mass lies inside the ring, which means it is not necessary that the Center of mass of a body lies in the body itself.
Finding the Center of Mass
Now, it is clear that bodies that are uniform and symmetrical have their Center of masses at their centroid. But for bodies that are not symmetrical and uniform, the answer is not that simple. The Center of mass for such bodies can be anywhere. To work out the Center of mass of a complex object. A weighted average of the locations of each mass of the body is taken.
Let’s say there is a body consisting of a set of masses “mi“, each at position ri, the location of the Center of mass rcm is given by the formula below.
Mrcm = m1r1 + m2r2 + ….
⇒ rcm = 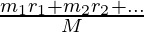
In this case, M =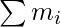 , which is the total mass of the body.
, which is the total mass of the body.
The above technique uses vector arithmetic. To avoid vector arithmetic, we can find out the Center of mass of the body along the x-axis and y-axis respectively. Formulas for this case are given below:
xcm = 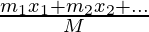
ycm = 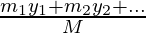
Center of Gravity
Usually, gravity is assumed to be a uniform force acting on the body. The Center of gravity is the point at which gravity is assumed to be acting on the body. The Center of gravity is thus at the same place as the Center of mass. In physics literature, the terms Center of gravity and Center of mass are used interchangeably. They mean the same thing.
Motion of the Center of Mass
Consider a system of multiple particles. Each particle of that system is moving at a different velocity. How would someone assign a velocity to the system as a whole? Let us consider a system of particles m1, m2, m3 …and so on. The initial position vectors of these particles are r1, r2, r3 …rn. Now, these particles start moving in the directions of their position vectors. The goal is to find the velocity and the direction of the velocity of the Center of mass of the system.
From the definition of the Center of mass,
Mrcm = m1r1 + m2r2 + ….
Since the particles are in motion, they are changing their position vectors. Differentiating the equation from both sides.
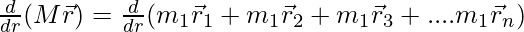
⇒ 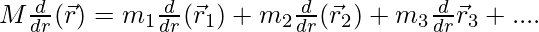
⇒ 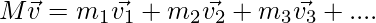
⇒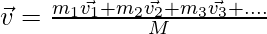
Similarly, if the particles are under acceleration. The equation given above can be differentiated again to find the acceleration of the Center of mass of the body.

Sample Problems
Question 1: Two point masses, m1 = 2Kg and m2 = 2Kg, are located moving at a speed of v1 = 2 m/s and v2 = 4 m/s respectively. Find the velocity of Center of mass.
Solution:
The formula for the velocity of the Center of mass is given by,
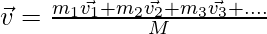
m1 = 2Kg, m2 = 2Kg and v1 = 2 m/s and v2 = 6 m/s.
M = m1 + m2
⇒ M = 2 + 2 = 4
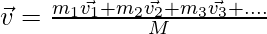
⇒ 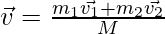
⇒ 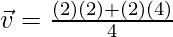
⇒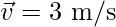
Question 2: Two-point masses, m1 = 10Kg and m2 = 20Kg, are located moving at a speed of v1 = 10 m/s and v2 = 5 m/s respectively. Find the velocity of the Center of mass.
Solution:
The formula for the velocity of the Center of mass is given by,
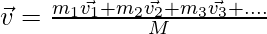
m1 = 10Kg, \m2 = 30Kg and v1 = 10 m/s and v2 = 5 m/s.
M = m1 + m2
⇒ M = 10 + 30 = 40
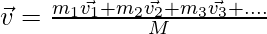
⇒ 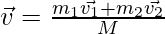
⇒ 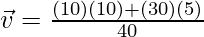
⇒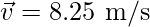
Question 3: Two–point masses, m1 = 1Kg and m2 = 2Kg, have velocity vectors a = 6i + 4j and vector b = -5i + 2j respectively. Find the velocity of Center of mass.
Solution:
The formula for the velocity of the Center of mass is given by,
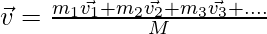
m1 = 1Kg, m2 = 2Kg and a = 6i + 4j, b = -5i + 2j
M = m1 + m2
⇒ M = 1 + 2 = 3
vcm = 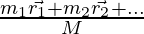
⇒vcm = 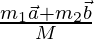
⇒ vcm = 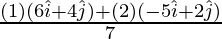
⇒ vcm = 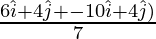
⇒ vcm = 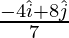
Question 4: Two–point masses, m1 = 4Kg and m2 = 2Kg, are located moving with velocity vectors a = i + j and vector b = -i + j respectively. Find the Center of mass.
Solution:
The formula for the velocity of Center of mass in the vector notation is given by,
vcm = 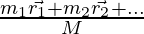
m1 = 4Kg, m2 = 2Kg and a = i + j, b = -i + j
M = m1 + m2
⇒ M = 4 + 2 = 6
vcm = 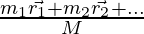
⇒vcm = 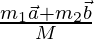
⇒ vcm = 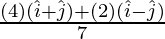
⇒ vcm = 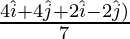
⇒ vcm = 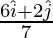
Question 5: A system consisting of two masses has a momentum of 16Kgm/s and its Center of mass has a velocity of 2 m/s. 4 Kg mass has a velocity of 4 m/s. Find the velocity of the other mass.
Solution:
The formula for the velocity of the Center of mass in the vector notation is given by,
vcm = 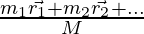
m2 = ?, m1 = 4Kg, v2 = ? And v1 = 4 m/s.
M = m1 + m2
⇒ M = 4 + m = 4 + m
Mvcm = 16
⇒ (m + 4)(2) = 16
⇒ m + 4 = 8
⇒m = 4Kg
Thus, m2 = 4Kg.
Mvcm = m1v1 + m2v2
⇒2(8) = (4)(4) + (4)v2
⇒ 16 = (4)(4) + (4)v2
⇒ 0 m/s = v2
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...