Motion Along a Rough Inclined Plane
Last Updated :
05 Aug, 2021
Friction is a force that resists the motion between two surfaces. While it is mostly responsible for resistance against motion, it is also responsible for motion. Without friction, no movement would be possible. When it comes to solid objects moving with respect to each other, there are mainly two types of friction – kinetic friction and static friction. This friction opposes the motion of the body kept on a surface. When it comes to the inclined planes, there are more than two forces acting on the body. It is essential to study friction and the resultant motion on such surfaces.
Friction
Frictional forces oppose motion between two objects. When it comes to solid objects, sitting on a rough surface. There are two types of friction that act on objects. These frictional forces depend on the type of surface and the forces being applied normally on the surface. The figure below shows the direction of the force and friction on a block kept on a rough surface. The friction force acting, in this case, can be of two types:
- Static Friction
- Kinetic Friction
Static Friction — This friction before the box starts moving. In this case, the friction is equal to the force applied. As the applied force increases, so does the friction. If the force keeps on increasing, the friction also increases, but there comes a point when the box starts moving. The point just before the box slips is called impeding motion. At this point, the static friction is maximum. It is determined by the coefficient of static friction 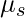
Formula for static friction
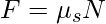
Kinetic Friction — Kinetic friction starts acting when the box starts moving. Its value is less than the maximum static friction. In this case, no matter what the applied force is, the value of the kinetic friction will remain the same. In this case, it is determined by the coefficient of kinetic friction 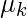
Formula for Kinetic friction:
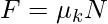

Motion on Rough Inclined Plane
The motion of a block on a rough inclined plane is the interplay of two different types of forces. The places on such a surface experience both the gravitational force and frictional force. While the gravitational forces trying to pull down the block, frictional force by its nature opposes the motion of the block. The figure below shows a block kept on a rough inclined plane. At this point, the block is at rest because the frictional forces can balance out the forces acting on the block.

Let us see the forces acting on the block. Gravitational force acts on the block in the downward direction. This force can split into two components, one which is acting parallel to the surface and another component which acts perpendicular to the surface of the plane. The component normal to the surface of the plane is responsible for the friction. The figure below shows the different forces acting on the block.

The free-body diagram given above can be used to find out the values of different components of the forces acting on the system. There is no motion in the direction perpendicular to the surface, which means the forces must be balanced in this direction.
Fy = mgsin(θ) – N = 0
Similarly, forces along the direction of the plane must be giving rise to the acceleration of the block. Assuming the mass of the block is “m” and its acceleration is “a”.
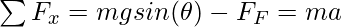
Here, FF is the force of friction. This can be maximum static friction, static friction, or kinetic friction. In this case, there can be a few possibilities based on the angle of inclination(θ).
Case (i): The friction is less than the maximum static friction and the body is yet to start the motion. In this case, 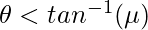 . In this case, friction is equal to the component of the force of gravity acting on the block.
. In this case, friction is equal to the component of the force of gravity acting on the block.
FF = mgsin(θ)
Case(ii): The friction is equal to maximum static friction and the body is yet to start the motion. Here 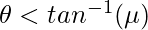 . In this case, too, the forces are balanced. Thus,
. In this case, too, the forces are balanced. Thus,
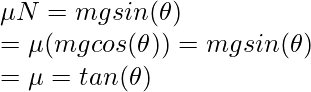
Case (iii): The friction is equal to kinetic friction. In this case, the body is in motion and the net force gives rise to the acceleration in the body. In this case,
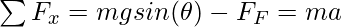
Where 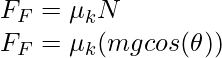
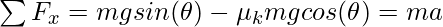
Sample Problems
Question 1: Find the value of the friction acting on a 5Kg block kept at rest on an inclined surface of angle 30°.
Answer:
Now, since the block is at rest, that means the forces in both the x and y directions must be balanced.
Net Force in the x-direction,
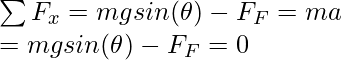
Force of friction is given by,
FF = mgsin(θ)
Given: m = 5Kg, θ = 30°
Plugging the values in the equation,
FF = mgsin(θ)
⇒ FF =(5)(10)sin(30°)
⇒ FF =25 N
Question 2: Find the value of the friction acting on a 10Kg block kept at rest on an inclined surface of angle 45°.
Answer:
Now, since the block is at rest, that means the forces in both the x and y directions must be balanced.
Net Force in the x-direction,
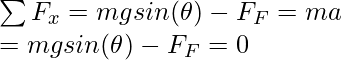
Force of friction is given by,
FF = mgsin(θ)
Given: m = 10Kg, θ = 45°
Plugging the values in the equation,
FF = mgsin(θ)
⇒ FF =(10)(10)sin(45°)
⇒ FF =50√2
⇒ FF = 50(1.414)
⇒ FF = 70.7 N
Question 3: Find the angle of the inclined surface at which the block kept on it will start slipping, given that the coefficient of static friction is 1.73.
Answer:
This is the case (ii) mentioned above. The block is just about to slip. In this case,
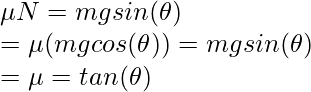
Given 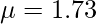
Plugging into the equation above,
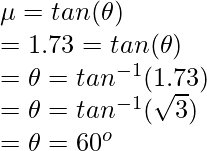
Question 4: Find the angle of the inclined surface at which the block kept on it will start slipping, given that the coefficient of static friction is 1.73.
Answer:
This is the case (ii) mentioned above. The block is just about to slip. In this case,
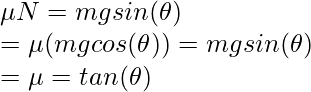
Given 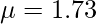
Plugging into the equation above,
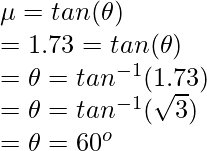
Question 5: Find the acceleration of a block( m = 50Kg) kept on an inclined plane of angle 60°. Given 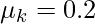
Answer:
tan(60) = √3 = 1.7313
Since tan(θ) > 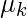
This is the case (iiI) mentioned above. The block will slip in this case,
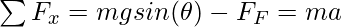
Where 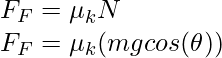
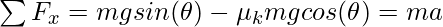
Given: 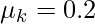 , m = 50Kg and θ = 60°.
, m = 50Kg and θ = 60°.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...