Modulus of a Complex Number

Given a complex number z, the task is to determine the modulus of this complex number. Note: Given a complex number z = a + ib the modulus is denoted by |z| and is defined as 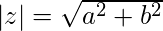Examples:

Input: z = 3 + 4i 
Output: 5 |z| = (3² + 4²)^1/2 = (9 + 16)^1/2 = 5 

Input: z = 6 – 8i 
Output: 10 
Explanation: |z| = (6² + (-8)²)^1/2 = (36 + 64)^1/2 = 10

Approach: For the given complex number z = x + iy:

1. Find the real and imaginary parts, x and y respectively.

If z = x +iy

Real part = x
Imaginary part = y

1. Find the square of x and y separately.

Square of Real part = x2
Square of Imaginary part = y2

1. Find the sum of the computed squares.

Sum = Square of Real part 
      + Square of Imaginary part
    = x2 + y2

1. Find the square root of the computed sum. This will be the modulus of the given complex number

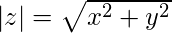
Below is the implementation of the above approach: 

C++

// C++ program to find the
// Modulus of a Complex Number

#include <bits/stdc++.h>
using namespace std;

// Function to find modulus
// of a complex number
void findModulo(string s)
{
    int l = s.length();
    int i, modulus = 0;

    // Storing the index of '+'
    if (s.find('+') < l) {
        i = s.find('+');
    }
    // Storing the index of '-'
    else {
        i = s.find('-');
    }

    // Finding the real part
    // of the complex number
    string real = s.substr(0, i);

    // Finding the imaginary part
    // of the complex number
    string imaginary = s.substr(i + 1, l - 1);

    int x = stoi(real);
    int y = stoi(imaginary);

    cout << sqrt(x * x + y * y) << "\n";
}

// Driver code
int main()
{
    string s = "3+4i";

    findModulo(s);

    return 0;
}

Java

// Java program to find the
// Modulus of a Complex Number
import java.util.*;

class GFG{

// Function to find modulus
// of a complex number
static void findModulo(String s)
{
    int l = s.length();
    int i, modulus = 0;

    // Storing the index of '+'
    if (s.contains("+")) {
        i = s.indexOf("+");
    }

    // Storing the index of '-'
    else {
        i = s.indexOf("-");
    }

    // Finding the real part
    // of the complex number
    String real = s.substring(0, i);

    // Finding the imaginary part
    // of the complex number
    String imaginary = s.substring(i + 1, l-1);

    int x = Integer.parseInt(real);
    int y = Integer.parseInt(imaginary);

    System.out.print(Math.sqrt(x * x + y * y)+ "\n");
}

// Driver code
public static void main(String[] args)
{
    String s = "3+4i";

    findModulo(s);
}
}

// This code is contributed by Rajput-Ji

Python 3

# Python 3 program to find the
# Modulus of a Complex Number
from math import sqrt

# Function to find modulus
# of a complex number
def findModulo(s):
    l = len(s)
    modulus = 0

    # Storing the index of '+'
    if ( '+' in s ):
        i = s.index('+')

    # Storing the index of '-'
    else:
        i = s.index('-')

    # Finding the real part
    # of the complex number
    real = s[0:i]

    # Finding the imaginary part
    # of the complex number
    imaginary = s[i + 1:l - 1]

    x = int(real)
    y = int(imaginary)

    print(int(sqrt(x * x + y * y)))

# Driver code
if __name__ == '__main__':
    s = "3+4i"

    findModulo(s)

# This code is contributed by Surendra_Gangwar

C#

// C# program to find the
// Modulus of a Complex Number
using System;

public class GFG{

// Function to find modulus
// of a complex number
static void findModulo(String s)
{
    int l = s.Length;
    int i;

    // Storing the index of '+'
    if (s.Contains("+")) {
        i = s.IndexOf("+");
    }

    // Storing the index of '-'
    else {
        i = s.IndexOf("-");
    }

    // Finding the real part
    // of the complex number
    String real = s.Substring(0, i);

    // Finding the imaginary part
    // of the complex number
    String imaginary = s.Substring(i + 1, l-i - 2);

    int x = Int32.Parse(real);
    int y = Int32.Parse(imaginary);

    Console.Write(Math.Sqrt(x * x + y * y)+ "\n");
}

// Driver code
public static void Main(String[] args)
{
    String s = "3+4i";

    findModulo(s);
}
}
// This code contributed by sapnasingh4991

Javascript

// JavaScript program to find the
// Modulus of a Complex Number

// Function to find modulus
// of a complex number
function findModulo(s)
{
    let l = s.length;
    let i, modulus = 0;

    // Storing the index of '+'
    if (s.indexOf('+')< l) {
        i = s.indexOf('+');
    }
    // Storing the index of '-'
    else {
        i = s.indexOf('-');
    }

    // Finding the real part
    // of the complex number
    let real = s.substring(0, i);

    // Finding the imaginary part
    // of the complex number
    let imaginary = s.substring(i + 1, l - 1);

    let x = parseInt(real);
    let y = parseInt(imaginary);

    console.log(Math.sqrt(x*x + y*y));
}

// Driver code
let s = "3+4i";
findModulo(s);

// The code is contributed by Gautam goel (gautamgoel962)

Output:

5

Time Complexity: O(1)
Auxiliary Space: O(1)

As constant extra space is used