ML | Using SVM to perform classification on a non-linear dataset
Last Updated :
15 Jan, 2019
Prerequisite: Support Vector Machines
Definition of a hyperplane and SVM classifier:
For a linearly separable dataset having n features (thereby needing n dimensions for representation), a hyperplane is basically an (n – 1) dimensional subspace used for separating the dataset into two sets, each set containing data points belonging to a different class. For example, for a dataset having two features X and Y (therefore lying in a 2-dimensional space), the separating hyperplane is a line (a 1-dimensional subspace). Similarly, for a dataset having 3-dimensions, we have a 2-dimensional separating hyperplane, and so on.
In machine learning, Support Vector Machine (SVM) is a non-probabilistic, linear, binary classifier used for classifying data by learning a hyperplane separating the data.
Classifying a non-linearly separable dataset using a SVM – a linear classifier:
As mentioned above SVM is a linear classifier which learns an (n – 1)-dimensional classifier for classification of data into two classes. However, it can be used for classifying a non-linear dataset. This can be done by projecting the dataset into a higher dimension in which it is linearly separable!
To get a better understanding, let’s consider circles dataset.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from mpl_toolkits.mplot3d import Axes3D
X, Y = make_circles(n_samples = 500, noise = 0.02)
plt.scatter(X[:, 0], X[:, 1], c = Y, marker = '.')
plt.show()
|
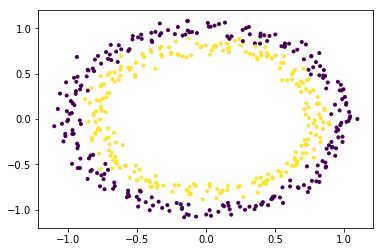
The dataset is clearly a non-linear dataset and consists of two features (say, X and Y).
In order to use SVM for classifying this data, introduce another feature Z = X2 + Y2 into the dataset. Thus, projecting the 2-dimensional data into 3-dimensional space. The first dimension representing the feature X, second representing Y and third representing Z (which, mathematically, is equal to the radius of the circle of which the point (x, y) is a part of). Now, clearly, for the data shown above, the ‘yellow’ data points belong to a circle of smaller radius and the ‘purple’ data points belong to a circle of larger radius. Thus, the data becomes linearly separable along the Z-axis.
X1 = X[:, 0].reshape((-1, 1))
X2 = X[:, 1].reshape((-1, 1))
X3 = (X1**2 + X2**2)
X = np.hstack((X, X3))
fig = plt.figure()
axes = fig.add_subplot(111, projection = '3d')
axes.scatter(X1, X2, X1**2 + X2**2, c = Y, depthshade = True)
plt.show()
|
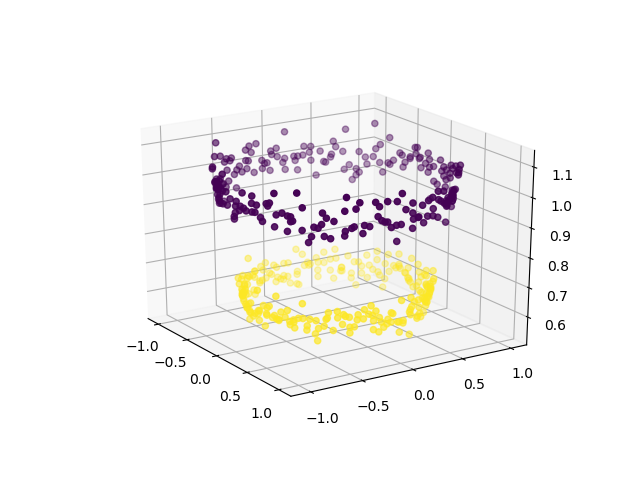
Now, we can use SVM (or, for that matter, any other linear classifier) to learn a 2-dimensional separating hyperplane. This is how the hyperplane would look like:
from sklearn import svm
svc = svm.SVC(kernel = 'linear')
svc.fit(X, Y)
w = svc.coef_
b = svc.intercept_
x1 = X[:, 0].reshape((-1, 1))
x2 = X[:, 1].reshape((-1, 1))
x1, x2 = np.meshgrid(x1, x2)
x3 = -(w[0][0]*x1 + w[0][1]*x2 + b) / w[0][2]
fig = plt.figure()
axes2 = fig.add_subplot(111, projection = '3d')
axes2.scatter(X1, X2, X1**2 + X2**2, c = Y, depthshade = True)
axes1 = fig.gca(projection = '3d')
axes1.plot_surface(x1, x2, x3, alpha = 0.01)
plt.show()
|
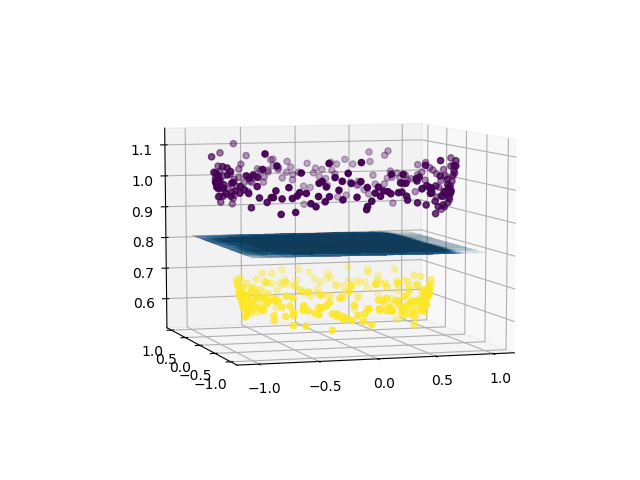
Thus, using a linear classifier we can separate a non-linearly separable dataset.
A brief introduction to kernels in machine learning:
In machine learning, a trick known as “kernel trick” is used to learn a linear classifier to classify a non-linear dataset. It transforms the linearly inseparable data into a linearly separable one by projecting it into a higher dimension. A kernel function is applied on each data instance to map the original non-linear data points into some higher dimensional space in which they become linearly separable.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...