ML | Ridge Regressor using sklearn

A Ridge regressor is basically a regularized version of a Linear Regressor. i.e to the original cost function of linear regressor we add a regularized term that forces the learning algorithm to fit the data and helps to keep the weights lower as possible. The regularized term has the parameter ‘alpha’ which controls the regularization of the model i.e helps in reducing the variance of the estimates. 
Cost Function for Ridge Regressor. 

(1)

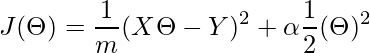
Here, 
The first term is our basic linear regression’s cost function and the second term is our new regularized weights term which uses the L2 norm to fit the data. If the ‘alpha’ is zero the model is the same as linear regression and the larger ‘alpha’ value specifies a stronger regularization. 
Note: Before using Ridge regressor it is necessary to scale the inputs, because this model is sensitive to scaling of inputs. So performing the scaling through sklearn’s StandardScalar will be beneficial. 
Code : Python code for implementing Ridge Regressor.

Python3

# importing libraries
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler

# loading boston dataset
boston = load_boston()
X = boston.data[:, :13]
y = boston.target

print ("Boston dataset keys : \n", boston.keys())

print ("\nBoston data : \n", boston.data)

# scaling the inputs
scaler = StandardScaler()
scaled_X = scaler.fit_transform(X)

# Train Test split will be used for both models
X_train, X_test, y_train, y_test = train_test_split(scaled_X, y,
                                                    test_size = 0.3)

# training model with 0.5 alpha value
model = Ridge(alpha = 0.5, normalize = False, tol = 0.001, \
              solver ='auto', random_state = 42)
model.fit(X_train, y_train)

# predicting the y_test
y_pred = model.predict(X_test)

# finding score for our model
score = model.score(X_test, y_test)
print("\n\nModel score : ", score)

Output : 

Boston dataset keys : 
 dict_keys(['feature_names', 'DESCR', 'data', 'target'])

Boston data : 
 [[6.3200e-03 1.8000e+01 2.3100e+00 ... 1.5300e+01 3.9690e+02 4.9800e+00]
 [2.7310e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9690e+02 9.1400e+00]
 [2.7290e-02 0.0000e+00 7.0700e+00 ... 1.7800e+01 3.9283e+02 4.0300e+00]
 ...
 [6.0760e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 5.6400e+00]
 [1.0959e-01 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9345e+02 6.4800e+00]
 [4.7410e-02 0.0000e+00 1.1930e+01 ... 2.1000e+01 3.9690e+02 7.8800e+00]]


Model score :  0.6819292026260749

A newer version RidgeCV comes with built-in Cross-Validation for an alpha, so definitely better. Only pass the array of some alpha range values and it’ll automatically choose the optimal value for ‘alpha’.
Note : ‘tol’ is the parameter which measures the loss drop and ensures to stop the model at that provided value position or drop at(global minima value).