ML | MultiLabel Ranking Metrics – Coverage Error

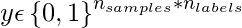
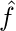
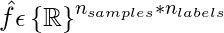
The coverage error tells us how many top-scored final prediction labels we have to include without missing any ground truth label. This is useful if we want to know the average number of top-scored-prediction required to predict in order to not miss any ground truth label. Given a binary indicator matrix of ground-truth labels . 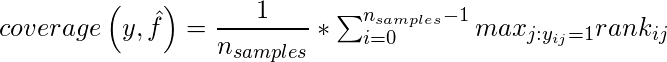The score associated with each label is denoted by where, The coverage error is defined as: where rank is defined as 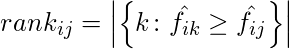Code: To check for coverage Error for any prediction scores with true-labels using scikit-learn.

# Import dataset
import numpy as np
from sklearn.metrics import coverage_error

# Create Imaginary prediction and truth dataset
y_true = np.array([[1, 0, 1], [0, 0, 1], [0, 1, 1]])
y_pred_score = np.array([[0.75, 0.5, 1], [1, 1, 1.2], [2.3, 1.2, 0.1]])
print(coverage_error(y_true, y_pred_score))

Output:

coverage error of 2.0

Let’s calculate the coverage error of above example manually Our first sample has ground-truth value of [1, 0, 1]. To cover both true labels we need to look our predictions (here [0.75, 0.5, 1]) into descending order. Thus, we need top-2 predicted labels in this sample. Similarly for second and third samples, we need top-1 and top-2 predicted samples. Averaging these results over a number of samples gives us an output of 2.0. 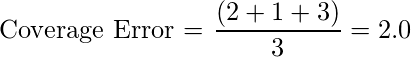The best value of coverage is when it is equal to average number of true class labels.