ML | Monte Carlo Tree Search (MCTS)
Last Updated :
23 May, 2023
Introduction :
Monte Carlo Tree Search (MCTS) is a heuristic search set of rules that has won big attention and reputation within the discipline of synthetic intelligence, specially in the area of choice-making and game playing. It is known for its ability to effectively handle complex and strategic video games with massive search areas, in which traditional algorithms may additionally struggle due to the full-size number of feasible actions or actions.
MCTS combines the standards of Monte Carlo strategies, which rely upon random sampling and statistical evaluation, with tree-primarily based search techniques. Unlike traditional search algorithms that rely upon exhaustive exploration of the entire seek area, MCTS specializes in sampling and exploring only promising areas of the hunt area.
The center idea in the back of MCTS is to build a seek tree incrementally by using simulating more than one random performs (regularly known as rollouts or playouts) from the current recreation nation. These simulations are carried out until a terminal state or a predefined intensity is reached. The results of these simulations are then backpropagated up the tree, updating the records of the nodes visited at some stage in the play, which includes the wide variety of visits and the win ratios.
As the search progresses, MCTS dynamically balances exploration and exploitation. It selects moves through considering both the exploitation of notably promising movements with high win ratios and the exploration of unexplored or less explored moves. This balancing is finished through the usage of an top confidence sure (UCB) components, which includes the Upper Confidence Bounds for Trees (UCT), to decide which moves or nodes to visit for the duration of the hunt.
MCTS has been efficiently implemented in numerous domains, including board games (e.G., Go, chess, and shogi), card video games (e.G., poker), and video games. It has done splendid overall performance in lots of challenging recreation-gambling scenarios, frequently surpassing human understanding. MCTS has also been prolonged and tailored to deal with different trouble domains, which include making plans, scheduling, and optimization.
One of the exquisite blessings of MCTS is its ability to handle video games with unknown or imperfect data, as it relies on statistical sampling as opposed to whole know-how of the game state. Additionally, MCTS is scalable and may be parallelized efficaciously, making it suitable for disbursed computing and multi-core architectures.
Monte Carlo Tree Search (MCTS) is a search technique in the field of Artificial Intelligence (AI). It is a probabilistic and heuristic driven search algorithm that combines the classic tree search implementations alongside machine learning principles of reinforcement learning.
In tree search, there’s always the possibility that the current best action is actually not the most optimal action. In such cases, MCTS algorithm becomes useful as it continues to evaluate other alternatives periodically during the learning phase by executing them, instead of the current perceived optimal strategy. This is known as the ” exploration-exploitation trade-off “. It exploits the actions and strategies that is found to be the best till now but also must continue to explore the local space of alternative decisions and find out if they could replace the current best.
Exploration helps in exploring and discovering the unexplored parts of the tree, which could result in finding a more optimal path. In other words, we can say that exploration expands the tree’s breadth more than its depth. Exploration can be useful to ensure that MCTS is not overlooking any potentially better paths. But it quickly becomes inefficient in situations with large number of steps or repetitions. In order to avoid that, it is balanced out by exploitation. Exploitation sticks to a single path that has the greatest estimated value. This is a greedy approach and this will extend the tree’s depth more than its breadth. In simple words, UCB formula applied to trees helps to balance the exploration-exploitation trade-off by periodically exploring relatively unexplored nodes of the tree and discovering potentially more optimal paths than the one it is currently exploiting.
For this characteristic, MCTS becomes particularly useful in making optimal decisions in Artificial Intelligence (AI) problems.
Why use Monte Carlo Tree Search (MCTS) ?
Here are some reasons why MCTS is commonly used:
- Handling Complex and Strategic Games: MCTS excels in games with large search spaces, complex dynamics, and strategic decision-making. It has been successfully applied to games like Go, chess, shogi, poker, and many others, achieving remarkable performance that often surpasses human expertise. MCTS can effectively explore and evaluate different moves or actions, leading to strong gameplay and decision-making in such games.
- Unknown or Imperfect Information: MCTS is suitable for games or scenarios with unknown or imperfect information. It relies on statistical sampling and does not require complete knowledge of the game state. This makes MCTS applicable to domains where uncertainty or incomplete information exists, such as card games or real-world scenarios with limited or unreliable data.
- Learning from Simulations: MCTS learns from simulations or rollouts to estimate the value of actions or states. Through repeated iterations, MCTS gradually refines its knowledge and improves decision-making. This learning aspect makes MCTS adaptive and capable of adapting to changing circumstances or evolving strategies.
- Optimizing Exploration and Exploitation: MCTS effectively balances exploration and exploitation during the search process. It intelligently explores unexplored areas of the search space while exploiting promising actions based on existing knowledge. This exploration-exploitation trade-off allows MCTS to find a balance between discovering new possibilities and exploiting known good actions.
- Scalability and Parallelization: MCTS is inherently scalable and can be parallelized efficiently. It can utilize distributed computing resources or multi-core architectures to speed up the search and handle larger search spaces. This scalability makes MCTS applicable to problems that require significant computational resources.
- Applicability Beyond Games: While MCTS gained prominence in game-playing domains, its principles and techniques are applicable to other problem domains as well. MCTS has been successfully applied to planning problems, scheduling, optimization, and decision-making in various real-world scenarios. Its ability to handle complex decision-making and uncertainty makes it valuable in a range of applications.
- Domain Independence: MCTS is relatively domain-independent. It does not require domain-specific knowledge or heuristics to operate. Although domain-specific enhancements can be made to improve performance, the basic MCTS algorithm can be applied to a wide range of problem domains without significant modifications.
Monte Carlo Tree Search (MCTS) algorithm:
In MCTS, nodes are the building blocks of the search tree. These nodes are formed based on the outcome of a number of simulations. The process of Monte Carlo Tree Search can be broken down into four distinct steps, viz., selection, expansion, simulation and backpropagation. Each of these steps is explained in details below:
- Selection: In this process, the MCTS algorithm traverses the current tree from the root node using a specific strategy. The strategy uses an evaluation function to optimally select nodes with the highest estimated value. MCTS uses the Upper Confidence Bound (UCB) formula applied to trees as the strategy in the selection process to traverse the tree. It balances the exploration-exploitation trade-off. During tree traversal, a node is selected based on some parameters that return the maximum value. The parameters are characterized by the formula that is typically used for this purpose is given below.
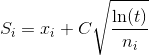
- where;
Si = value of a node i
xi = empirical mean of a node i
C = a constant
t = total number of simulations
When traversing a tree during the selection process, the child node that returns the greatest value from the above equation will be one that will get selected. During traversal, once a child node is found which is also a leaf node, the MCTS jumps into the expansion step.
- Expansion: In this process, a new child node is added to the tree to that node which was optimally reached during the selection process.
- Simulation: In this process, a simulation is performed by choosing moves or strategies until a result or predefined state is achieved.
- Backpropagation: After determining the value of the newly added node, the remaining tree must be updated. So, the backpropagation process is performed, where it backpropagates from the new node to the root node. During the process, the number of simulation stored in each node is incremented. Also, if the new node’s simulation results in a win, then the number of wins is also incremented.
The above steps can be visually understood by the diagram given below:
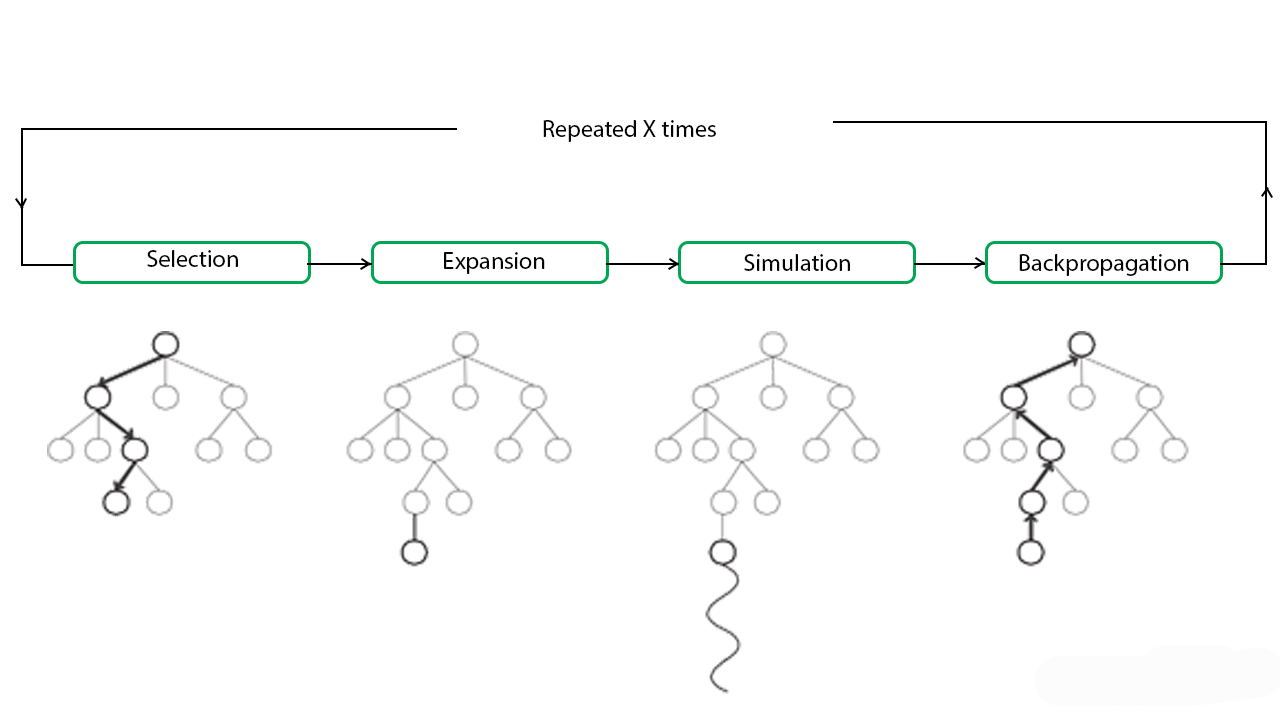
These types of algorithms are particularly useful in turn based games where there is no element of chance in the game mechanics, such as Tic Tac Toe, Connect 4, Checkers, Chess, Go, etc. This has recently been used by Artificial Intelligence Programs like AlphaGo, to play against the world’s top Go players. But, its application is not limited to games only. It can be used in any situation which is described by state-action pairs and simulations used to forecast outcomes.
Pseudo-code for Monte Carlo Tree search:
Python3
def monte_carlo_tree_search(root):
while resources_left(time, computational power):
leaf = traverse(root)
simulation_result = rollout(leaf)
backpropagate(leaf, simulation_result)
return best_child(root)
def traverse(node):
while fully_expanded(node):
node = best_uct(node)
return pick_unvisited(node.children) or node
def rollout(node):
while non_terminal(node):
node = rollout_policy(node)
return result(node)
def rollout_policy(node):
return pick_random(node.children)
def backpropagate(node, result):
if is_root(node) return
node.stats = update_stats(node, result)
backpropagate(node.parent)
def best_child(node):
pick child with highest number of visits
|
As we can see, the MCTS algorithm reduces to a very few set of functions which we can use any choice of games or in any optimizing strategy.
Advantages of Monte Carlo Tree Search:
- MCTS is a simple algorithm to implement.
- Monte Carlo Tree Search is a heuristic algorithm. MCTS can operate effectively without any knowledge in the particular domain, apart from the rules and end conditions, and can find its own moves and learn from them by playing random playouts.
- The MCTS can be saved in any intermediate state and that state can be used in future use cases whenever required.
- MCTS supports asymmetric expansion of the search tree based on the circumstances in which it is operating.
Disadvantages of Monte Carlo Tree Search:
- As the tree growth becomes rapid after a few iterations, it requires a huge amount of memory.
- There is a bit of a reliability issue with Monte Carlo Tree Search. In certain scenarios, there might be a single branch or path, that might lead to loss against the opposition when implemented for those turn-based games. This is mainly due to the vast amount of combinations and each of the nodes might not be visited enough number of times to understand its result or outcome in the long run.
- MCTS algorithm needs a huge number of iterations to be able to effectively decide the most efficient path. So, there is a bit of a speed issue there.
Issues in Monte Carlo Tree Search:
Here are some common issues associated with MCTS:
- Exploration-Exploitation Trade-off: MCTS faces the challenge of balancing exploration and exploitation during the search. It needs to explore different branches of the search tree to gather information about their potential, while also exploiting promising actions based on existing knowledge. Achieving the right balance is crucial for the algorithm’s effectiveness and performance.
- Sample Efficiency: MCTS can require a large number of simulations or rollouts to obtain accurate statistics and make informed decisions. This can be computationally expensive, especially in complex domains with a large search space. Improving the sample efficiency of MCTS is an ongoing research area.
- High Variance: The outcomes of individual rollouts in MCTS can be highly variable due to the random nature of the simulations. This can lead to inconsistent estimations of action values and introduce noise in the decision-making process. Techniques such as variance reduction and progressive widening are used to mitigate this issue.
- Heuristic Design: MCTS relies on heuristics to guide the search and prioritize actions or nodes. Designing effective and domain-specific heuristics can be challenging, and the quality of the heuristics directly affects the algorithm’s performance. Developing accurate heuristics that capture the characteristics of the problem domain is an important aspect of using MCTS.
- Computation and Memory Requirements: MCTS can be computationally intensive, especially in games with long horizons or complex dynamics. The algorithm’s performance depends on the available computational resources, and in resource-constrained environments, it may not be feasible to run MCTS with a sufficient number of simulations. Additionally, MCTS requires memory to store and update the search tree, which can become a limitation in memory-constrained scenarios.
- Overfitting: In certain cases, MCTS can overfit to specific patterns or biases present in the early simulations, which can lead to suboptimal decisions. To mitigate this issue, techniques such as exploration bonuses, progressive unpruning, and rapid action-value estimation have been proposed to encourage exploration and avoid premature convergence.
- Domain-specific Challenges: Different domains and problem types can introduce additional challenges and issues for MCTS. For example, games with hidden or imperfect information, large branching factors, or continuous action spaces require adaptations and extensions of the basic MCTS algorithm to handle these complexities effectively.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...