ML | Mathematical explanation of RMSE and R-squared error
Last Updated :
06 Jun, 2022
RMSE: Root Mean Square Error is the measure of how well a regression line fits the data points. RMSE can also be construed as Standard Deviation in the residuals.
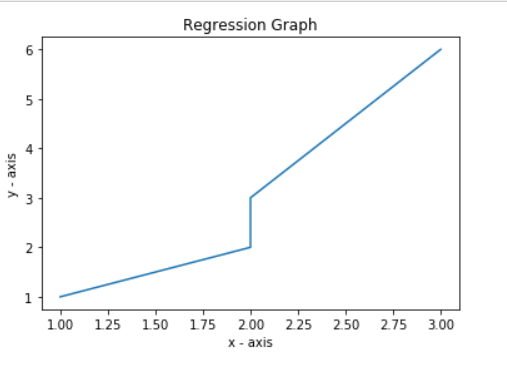
Consider the given data points: (1, 1), (2, 2), (2, 3), (3, 6).
Let us break the above data points into 1-d lists.
Input:
x = [1, 2, 2, 3]
y = [1, 2, 3, 6]
Code: Regression Graph
Python
import matplotlib.pyplot as plt
import math
plt.plot(x, y)
plt.xlabel('x - axis')
plt.ylabel('y - axis')
plt.title('Regression Graph')
plt.show()
|
Output:
Code: Mean Calculation
Python
ct = len(x)
sum_x = 0
sum_y = 0
for i in x:
sum_x = sum_x + i
x_mean = sum_x / ct
print('Value of X mean', x_mean)
for i in y:
sum_y = sum_y + i
y_mean = sum_y / ct
print('value of Y mean', y_mean)
|
Output :
Value of X mean 2.0
value of Y mean 3.0
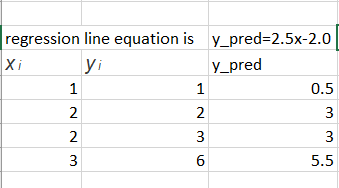
Code: Line Equation
Python
m = 2.5
c = y_mean - m * x_mean
print('Intercept', c)
|
Output:
Intercept -2.0
Code: Mean Squared Error
Python
from sklearn.metrics import mean_squared_error
y =[1, 2, 3, 6]
y_pred =[0.5, 3, 3, 5.5]
|
Output:
Python
mse1 = math.sqrt(mean_squared_error(y, y_pred))
print('Root mean square error', mse1)
mse2 = mean_squared_error(y, y_pred, squared=False)
print('Root mean square error', mse2)
|
Output:
Root mean square error 0.6123724356957945
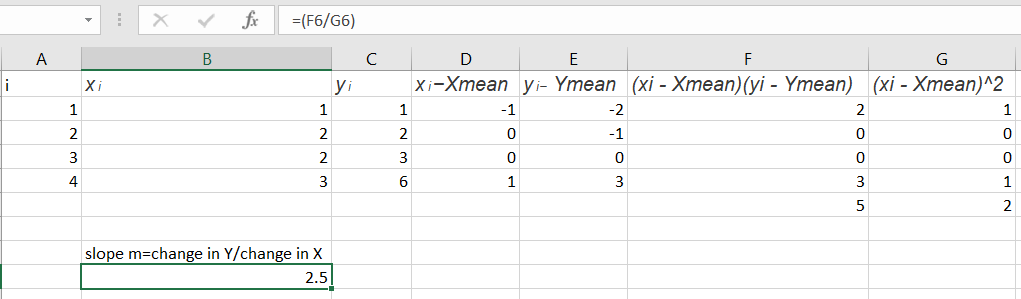
Code : RMSE Calculation
Python
r1 = 1-(2.5 * 1-2.0)
r2 = 2-(2.5 * 2-2.0)
r3 = 3-(2.5 * 2-2.0)
r4 = 6-(2.5 * 3-2.0)
residuals =[0.5, -1, 0, .5]
N = 4
rmse = math.sqrt((r1**2 + r2**2 + r3**2 + r4**2)/N)
print('Root Mean square error using maths', rmse)
|
Output:
Output:
Root Mean square error using maths 0.6123724356957945
R-squared Error or Coefficient of Determination
R2 error answers the below question.
How much y varies with variation in x.Basically the % variation of y on variation with x
Code: R-Squared Error
Python
val1 =(1-(2.5 * 1+(-2)))**2
val2 =(2-(2.5 * 2+(-2)))**2
val3 =(3-(2.5 * 2+(-2)))**2
val4 =(6-(2.5 * 3+(-2)))**2
SE_line = val1 + val2 + val3 + val4
print('val', val1, val2, val3, val4)
y =[1, 2, 3, 6]
y_var =(1-3)**2+(2-3)**2+(3-3)**2+(6-3)**2
SE_mean = y_var
r_squared = 1-(SE_line / SE_mean)
print('Rsquared error', r_squared)
|
Output
('val', 0.25, 1.0, 0.0, 0.25)
('Rsquared error', 0.8928571428571429)
Code: R-Squared Error with sklearn
Python
from sklearn.metrics import r2_score
r2_score(y, y_pred)
|
Output:
0.8928571428571429
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...