ML | Fowlkes-Mallows Score
Last Updated :
10 Jun, 2022
The Fowlkes-Mallows Score is an evaluation metric to evaluate the similarity among clusterings obtained after applying different clustering algorithms. Although technically it is used to quantify the similarity between two clusterings, it is typically used to evaluate the clustering performance of a clustering algorithm by assuming the second clustering to be the ground-truth ie the observed data and assuming it to be the perfect clustering. Let there be N number of data points in the data and k number of clusters in clusterings A1 and A2. Then the matrix M is built such that ![Rendered by QuickLaTeX.com M = [m_{ij}]_{k\times k}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8c44b09a853f38ab1663e68331d39ad3_l3.png) where
where 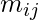 determines the number of data points that lie in the ith cluster in clustering A1 and the jth cluster in clustering A2. The Fowlkes-Mallows index for the parameter k is given by
determines the number of data points that lie in the ith cluster in clustering A1 and the jth cluster in clustering A2. The Fowlkes-Mallows index for the parameter k is given by 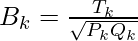 where
where 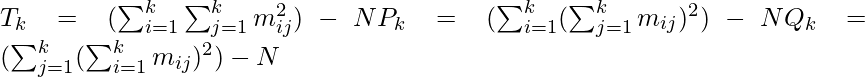 The following terms are defined in the context of the above-defined symbolic conventions:-
The following terms are defined in the context of the above-defined symbolic conventions:-
- True Positive(TP): The number of pair of data points which are in the same cluster in A1 and in A2.
- False Positive(FP): The number of pair of data points which are in the same cluster in A1 but not in A2.
- False Negative(FN): The number of pair of data points which are not in the same cluster in A1 but are in the same cluster in A2.
- True Negative(TN): The number of pair of data points which are not in the same cluster in neither A1 nor A2.
Obviously 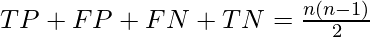 Thus the Fowlkes-Mallows Index can also be expressed as:-
Thus the Fowlkes-Mallows Index can also be expressed as:- 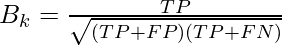 Rewriting the above expression
Rewriting the above expression 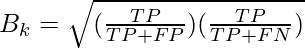 [Tex]\Rightarrow B_{k} = \sqrt{Precision\times Recall} [/Tex]Thus the Fowlkes-Mallows Index is the geometric mean of the precision and the recall. Properties:
[Tex]\Rightarrow B_{k} = \sqrt{Precision\times Recall} [/Tex]Thus the Fowlkes-Mallows Index is the geometric mean of the precision and the recall. Properties:
- Assumption-Less: This evaluation metric does not assume any property about the cluster structure thus proving to be significantly advantageous than traditional evaluation methods.
- Ground-Truth Rules: One disadvantage to this evaluation metric is that it requires the knowledge of the ground-truth rules(Class Labels) to evaluate a clustering algorithm.
The below steps will demonstrate how to evaluate the Fowlkes-Mallows Index for a clustering algorithm by using Sklearn. The dataset for the below steps is the Credit Card Fraud Detection dataset which can be downloaded from Kaggle. Step 1: Importing the required libraries
Python3
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import fowlkes_mallows
|
Step 2: Loading and Cleaning the data
Python3
cd C:\Users\Dev\Desktop\Kaggle\Credit Card Fraud
df = pd.read_csv('creditcard.csv')
y = df['Class']
X = df.drop('Class',axis=1)
X.head()
|
 Step 3: Building different Clustering and evaluating individual performances The following step lines of code involve Building different K-Means Clustering models each having different values for the parameter n_clusters and then evaluating each individual performance using the Fowlkes-Mallows Score.
Step 3: Building different Clustering and evaluating individual performances The following step lines of code involve Building different K-Means Clustering models each having different values for the parameter n_clusters and then evaluating each individual performance using the Fowlkes-Mallows Score.
Python3
fms_scores = []
N_Clusters = [2,3,4,5,6]
|
a) n_clusters = 2
Python3
kmeans2 = KMeans(n_clusters=2)
kmeans2.fit(X)
labels2 = kmeans2.predict(X)
fms_scores.append(fms(y,labels2))
|
b) n_clusters = 3
Python3
kmeans3 = KMeans(n_clusters=3)
kmeans3.fit(X)
labels3 = kmeans3.predict(X)
fms_scores.append(fms(y,labels3))
|
c) n_clusters = 4
Python3
kmeans4 = KMeans(n_clusters=4)
kmeans4.fit(X)
labels4 = kmeans4.predict(X)
fms_scores.append(fms(y,labels4))
|
d) n_clusters = 5
Python3
kmeans5 = KMeans(n_clusters=5)
kmeans5.fit(X)
labels5 = kmeans5.predict(X)
fms_scores.append(fms(y,labels5))
|
e) n_clusters = 6
Python3
kmeans6 = KMeans(n_clusters=6)
kmeans6.fit(X)
labels6 = kmeans6.predict(X)
fms_scores.append(fms(y,labels6))
|
 Step 4: Visualizing and Comparing the results
Step 4: Visualizing and Comparing the results
Python3
plt.bar(N_Clusters,fms_scores)
plt.xlabel('Number of Clusters')
plt.ylabel('Fowlkes Mallows Score')
plt.title('Comparison of different Clustering Models')
plt.show()
|
Thus, quite obviously, the clustering with the number of clusters = 2 is the most similar to the observed data because the data has only two class labels.
Share your thoughts in the comments
Please Login to comment...