ML | Determine the optimal value of K in K-Means Clustering
Last Updated :
12 Oct, 2021
Prerequisite: K-Means Clustering | Introduction
There is a popular method known as elbow method which is used to determine the optimal value of K to perform the K-Means Clustering Algorithm. The basic idea behind this method is that it plots the various values of cost with changing k. As the value of K increases, there will be fewer elements in the cluster. So average distortion will decrease. The lesser number of elements means closer to the centroid. So, the point where this distortion declines the most is the elbow point.

3 clusters are forming
In the above figure, its clearly observed that the distribution of points are forming 3 clusters. Now, let’s see the plot for the squared error(Cost) for different values of K.

Elbow is forming at K=3
Clearly the elbow is forming at K=3. So the optimal value will be 3 for performing K-Means.
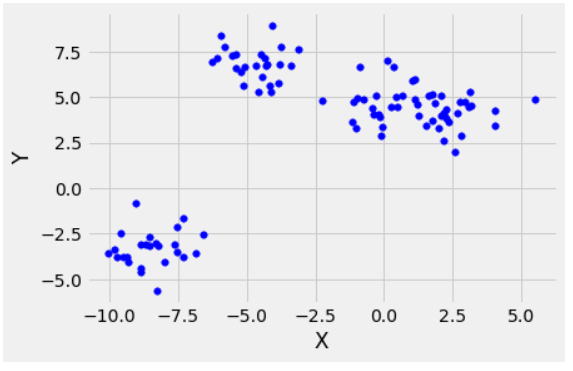
Another Example with 4 clusters.

4-clusters
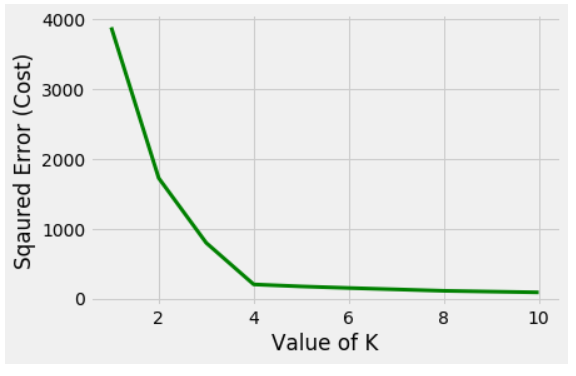
Corresponding Cost graph-

Elbow is forming at K=4
In this case the optimal value for k would be 4. (Observable from the scattered points).
Below is the Python implementation:
Python3
import matplotlib.pyplot as plt
from matplotlib import style
from sklearn.cluster import KMeans
from sklearn.datasets.samples_generator import make_blobs
style.use("fivethirtyeight")
X, y = make_blobs(n_samples = 100, centers = 4,
cluster_std = 1, n_features = 2)
plt.scatter(X[:, 0], X[:, 1], s = 30, color ='b')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
plt.clf()
|
Output:
Python3
cost =[]
for i in range(1, 11):
KM = KMeans(n_clusters = i, max_iter = 500)
KM.fit(X)
cost.append(KM.inertia_)
plt.plot(range(1, 11), cost, color ='g', linewidth ='3')
plt.xlabel("Value of K")
plt.ylabel("Squared Error (Cost)")
plt.show()
|
Output:
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...