Bias-Variance Trade Off – Machine Learning
Last Updated :
05 Jun, 2023
It is important to understand prediction errors (bias and variance) when it comes to accuracy in any machine-learning algorithm. There is a tradeoff between a model’s ability to minimize bias and variance which is referred to as the best solution for selecting a value of Regularization constant. A proper understanding of these errors would help to avoid the overfitting and underfitting of a data set while training the algorithm.
What is Bias?
The bias is known as the difference between the prediction of the values by the Machine Learning model and the correct value. Being high in biasing gives a large error in training as well as testing data. It recommended that an algorithm should always be low-biased to avoid the problem of underfitting. By high bias, the data predicted is in a straight line format, thus not fitting accurately in the data in the data set. Such fitting is known as the Underfitting of Data. This happens when the hypothesis is too simple or linear in nature. Refer to the graph given below for an example of such a situation.

High Bias in the Model
In such a problem, a hypothesis looks like follows.
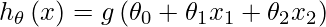
What is Variance?
The variability of model prediction for a given data point which tells us the spread of our data is called the variance of the model. The model with high variance has a very complex fit to the training data and thus is not able to fit accurately on the data which it hasn’t seen before. As a result, such models perform very well on training data but have high error rates on test data. When a model is high on variance, it is then said to as Overfitting of Data. Overfitting is fitting the training set accurately via complex curve and high order hypothesis but is not the solution as the error with unseen data is high. While training a data model variance should be kept low. The high variance data looks as follows.

High Variance in the Model
In such a problem, a hypothesis looks like follows.

Bias Variance Tradeoff
If the algorithm is too simple (hypothesis with linear equation) then it may be on high bias and low variance condition and thus is error-prone. If algorithms fit too complex (hypothesis with high degree equation) then it may be on high variance and low bias. In the latter condition, the new entries will not perform well. Well, there is something between both of these conditions, known as a Trade-off or Bias Variance Trade-off. This tradeoff in complexity is why there is a tradeoff between bias and variance. An algorithm can’t be more complex and less complex at the same time. For the graph, the perfect tradeoff will be like this.
We try to optimize the value of the total error for the model by using the Bias-Variance Tradeoff.

The best fit will be given by the hypothesis on the tradeoff point. The error to complexity graph to show trade-off is given as –
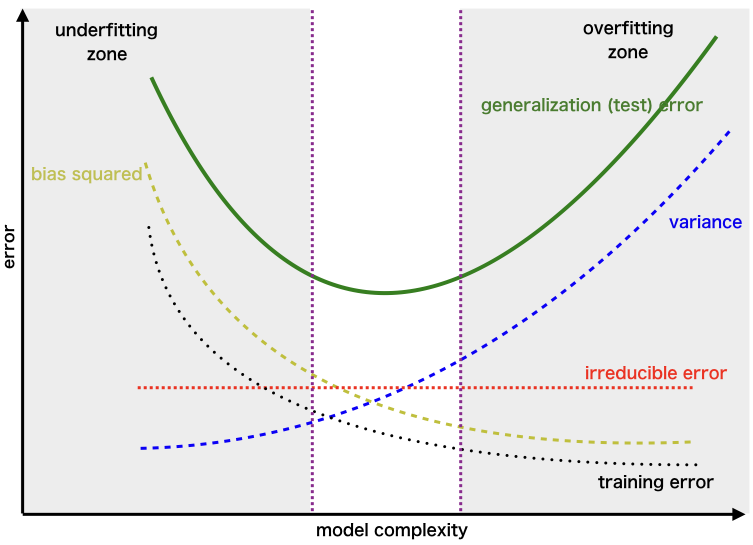
Region for the Least Value of Total Error
This is referred to as the best point chosen for the training of the algorithm which gives low error in training as well as testing data.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...