Minimum volume of cone that can be circumscribed about a sphere of radius R

Given a sphere of radius R, The task is to find out the minimum volume of the cone that can be circumscribed about it.

Examples:

Input: R = 10 
Output: Volume of cone = 8373.33 
Explanation: 
Radius of cone = 14.14 and Height of cone = 40,
Volume of cone = 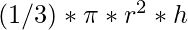So, volume = 8373.33Input: R = 4 Output: Volume of cone = 535.89 

Approach:
we have given a sphere of radius R inscribed in Cone. We need to find out the radius and height of the cone to find out the volume of the cone. 

1. 
   In triangle AOE and ALC compute sin(X) i.e. For triangle AOE 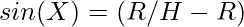and for triangle ALC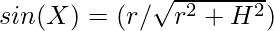 
   
2. 
   Now, From equating both we get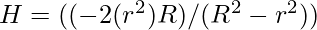 
   
3. 
   Insert the value of H in Volume i.e. 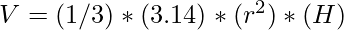and for volume to be minimum . 
   
4. 
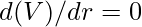   From the above equation we get 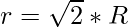and putting this value in H we get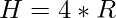
   
5. 
   Hence, applying the formula of volume of cone and putting 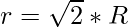and 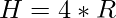we get the desired result. 
   

C++

// C++ program to find the minimum
// volume of the cone that can be
// circumscribed about a sphere
// of radius R
#include<bits/stdc++.h>
using namespace std;

// Function to find the volume
// of the cone
float Volume_of_cone(float R)
{

    // r = radius of cone
    // h = height of cone
    // Volume of cone = (1 / 3) * (3.14) * (r*r) * (h)
    // we get radius of cone from the derivation
    // is root(2) times multiple of R
    // we get height of cone from the derivation
    // is 4 times multiple of R
    float V = (1 / 3.0) * (3.14) * (2 * ( R * R ) ) * (4 * R);

    return V;
}

// Driver code
int main()
{
    float R = 10.0;
    cout << Volume_of_cone(R);
}

// This code is contributed by Samarth

Java

// Java program to find the minimum
// volume of the cone that can be
// circumscribed about a sphere
// of radius R
import java.util.*;

class GFG{

// Function to find the volume
// of the cone
static double Volume_of_cone(double R)
{

    // r = radius of cone
    // h = height of cone
    // Volume of cone = (1 / 3) * (3.14) * (r*r) * (h)
    // we get radius of cone from the derivation
    // is root(2) times multiple of R
    // we get height of cone from the derivation
    // is 4 times multiple of R
    double V = (double)((1 / 3.0) * (3.14) * (2 * (R * R)) *
                                                  (4 * R));
    return V;
}

// Driver code
public static void main(String[] args)
{
    double R = 10.0;
    System.out.print(Volume_of_cone(R));
}
}

// This code is contributed by sapnasingh4991

Python3

# Python3 program to find the minimum
# Volume of the cone that can be circumscribed
# about a sphere of radius R

import math

# Function to find the volume
# of the cone

def Volume_of_cone(R):

    # r = radius of cone
    # h = height of cone
    # Volume of cone = (1 / 3) * (3.14) * (r**2) * (h)
    # we get radius of cone from the derivation
    # is root(2) times multiple of R
    # we get height of cone from the derivation
    # is 4 times multiple of R

    V = (1 / 3) * (3.14) * (2 * ( R**2 ) ) * (4 * R)

    return V


# Driver code
if __name__ == "__main__":

    R = 10

    print(Volume_of_cone(R))

C#

// C# program to find the minimum
// volume of the cone that can be
// circumscribed about a sphere
// of radius R
using System;
class GFG{

// Function to find the volume
// of the cone
static double Volume_of_cone(double R)
{

    // r = radius of cone
    // h = height of cone
    // Volume of cone = (1 / 3) * (3.14) * (r*r) * (h)
    // we get radius of cone from the derivation
    // is root(2) times multiple of R
    // we get height of cone from the derivation
    // is 4 times multiple of R
    double V = (double)((1 / 3.0) * (3.14) *
                    (2 * (R * R)) * (4 * R));
    return V;
}

// Driver code
public static void Main()
{
    double R = 10.0;
    Console.Write(Volume_of_cone(R));
}
}

// This code is contributed by Nidhi_biet

Javascript

<script>
// Javascript program to find the minimum
// volume of the cone that can be
// circumscribed about a sphere
// of radius R

    // Function to find the volume
    // of the cone
    function Volume_of_cone( R)
    {

        // r = radius of cone
        // h = height of cone
        // Volume of cone = (1 / 3) * (3.14) * (r*r) * (h)
        // we get radius of cone from the derivation
        // is root(2) times multiple of R
        // we get height of cone from the derivation
        // is 4 times multiple of R
        let V =  ((1 / 3.0) * (3.14) * (2 * (R * R)) * (4 * R));
        return V;
    }

    // Driver code
    let R = 10.0;
    document.write(Volume_of_cone(R));

// This code is contributed by 29AjayKumar
</script>

Output:

8373.333333333332

Time complexity: O(1) since performing constant operations

Auxiliary space: O(1) since using constant variables