Minimum value possible of a given function from the given set
Last Updated :
26 Jul, 2022
Given a set Sn that represents a finite set {1, 2, 3, ….., n}. Zn denotes the set of all subsets of Sn which contains exactly 2 elements. The task is to find the value of F(n).
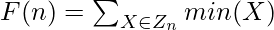
Examples:
Input: N = 3
Output: 4
For n=3 we get value 1, 2 times and 2, 1 times
thus the answer would be 1 * 2 + 2 * 1 = 4.
Input: N = 10
Output: 165
For each value as we go from left to right in the set we get each value, n-value number of times that value.
i.e. For each i, value to be added is (i + 1) * (n – i – 1)
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define ll long long
ll findF_N(ll n)
{
ll ans = 0;
for (ll i = 0; i < n; ++i)
ans += (i + 1) * (n - i - 1);
return ans;
}
int main()
{
ll n = 3;
cout << findF_N(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static long findF_N(long n)
{
long ans = 0;
for (long i = 0; i < n; ++i)
ans += (i + 1) * (n - i - 1);
return ans;
}
public static void main(String[] args)
{
long n = 3;
System.out.println(findF_N(n));
}
}
|
Python3
def findF_N(n):
ans = 0
for i in range(n):
ans = ans + (i + 1) * (n - i - 1)
return ans
n = 3
print(findF_N(n))
|
C#
using System;
class GFG {
static long findF_N(long n)
{
long ans = 0;
for (long i = 0; i < n; ++i)
ans += (i + 1) * (n - i - 1);
return ans;
}
public static void Main()
{
long n = 3;
Console.WriteLine(findF_N(n));
}
}
|
PHP
<?php
function findF_N($n)
{
$ans = 0;
for ($i = 0; $i < $n; ++$i)
$ans += ($i + 1) * ($n - $i - 1);
return $ans;
}
$n = 3;
echo findF_N($n);
|
Javascript
<script>
function findF_N(n)
{
var ans = 0;
for (var i = 0; i < n; ++i)
ans += (i + 1) * (n - i - 1);
return ans;
}
var n = 3;
document.write( findF_N(n));
</script>
|
Time Complexity: O(n) // n is the length of the array
Space Complexity: O(1)
Share your thoughts in the comments
Please Login to comment...