Minimum value of distance of farthest node in a Graph
Last Updated :
09 Aug, 2021
Given an acyclic undirected graph having N nodes and N-1 edges in the form of a 2D array arr[][] in which every row consists of two numbers L and R which denotes the edge between L and R. For every node X in the tree, let dis(X) denotes the number of edges from X to the farthest node. The task is to find the minimum value of dis(x) for the given graph.
Examples:
Input: N = 6, arr[][] = { {1, 4}, {2, 3}, {3, 4}, {4, 5}, {5, 6} }
Output: 2
Explanation:
Below is the graph from the above information:
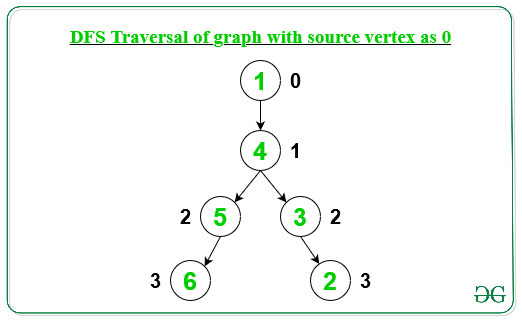
As we can see from the above graph the farthest node from vertex 0 is at distance 3. By repeating the DFS traversal for all the node in the graph, we have maximum distance[] from source node to farthest node as:
distance[] = {3, 4, 3, 2, 3, 4} and the minimum of the distances is the required result.
Input: N = 6, arr[][] = { {1, 2}, {1, 3}, {1, 4}, {2, 5}, {2, 6} }
Output: 2
Explanation:
The distance[] from every node to farthest node for the above graph is:
distance[] = {3, 4, 3, 2, 3, 4} and the minimum of the distances is 1.
Approach:
The idea is to use DFS Traversal to solve this problem. Below are the steps:
- For any Node(say a) traverse the graph using DFS Traversal with the distance of node with itself as 0.
- For every recursive call for Node a, keep updating the distance of the recursive node with the node a in an array(say distance[]).
- By taking the maximum of the distance with every recursive call for Node a give the number of edges between the nodes a and it’s farthest node.
- Repeat the above steps for all the node in the graph and keep updating the farthest node distance from every node in the distance array(distance[]).
- The minimum value of the array distance[] is the desired result.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> dist;
vector<int> vis;
void dfs(int u, vector<int> Adj[], int s)
{
vis[u] = true;
for (auto& it : Adj[u]) {
if (vis[it] == false) {
dfs(it, Adj, s + 1);
}
}
dist[u] = max(dist[u], s);
}
void minFarthestDistance(int arr[][2], int n)
{
dist.resize(n + 1, 0);
vector<int> Adj[n + 1];
for (int i = 0; i < n - 1; i++) {
Adj[arr[i][0]].push_back(arr[i][1]);
Adj[arr[i][1]].push_back(arr[i][0]);
}
for (int i = 1; i <= n; i++) {
vis.clear();
vis.resize(n + 1, false);
dfs(i, Adj, 0);
}
cout << *min_element(dist.begin() + 1,
dist.end());
}
int main()
{
int N = 6;
int arr[][2] = { { 1, 4 }, { 2, 3 }, { 3, 4 },
{ 4, 5 }, { 5, 6 } };
minFarthestDistance(arr, N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int[] dist;
static boolean[] vis;
static void dfs(int u, Vector<Integer>[] Adj, int s)
{
vis[u] = true;
for (int it : Adj[u])
{
if (vis[it] == false)
{
dfs(it, Adj, s + 1);
}
}
dist[u] = Math.max(dist[u], s);
}
static void minFarthestDistance(int[][] arr, int n)
{
dist = new int[n + 1];
Arrays.fill(dist, 0);
@SuppressWarnings("unchecked")
Vector<Integer>[] Adj = new Vector[n + 1];
for(int i = 0; i < n + 1; i++)
{
Adj[i] = new Vector<>();
}
for(int i = 0; i < n - 1; i++)
{
Adj[arr[i][0]].add(arr[i][1]);
Adj[arr[i][1]].add(arr[i][0]);
}
for(int i = 1; i <= n; i++)
{
vis = new boolean[n + 1];
Arrays.fill(vis, false);
dfs(i, Adj, 0);
}
int min = Integer.MAX_VALUE;
for(int i = 1; i < dist.length; i++)
{
if (dist[i] < min)
min = dist[i];
}
System.out.println(min);
}
public static void main(String[] args)
{
int N = 6;
int[][] arr = { { 1, 4 }, { 2, 3 },
{ 3, 4 }, { 4, 5 },
{ 5, 6 } };
minFarthestDistance(arr, N);
}
}
|
Python3
def dfs(u, s):
global vis, Adj, dist
vis[u] = True
for it in Adj[u]:
if (vis[it] == False):
dfs(it, s + 1)
dist[u] = max(dist[u], s)
def minFarthestDistance(arr, n):
global dist, vis, Adj
for i in range(n - 1):
Adj[arr[i][0]].append(arr[i][1])
Adj[arr[i][1]].append(arr[i][0])
for i in range(1, n + 1):
for j in range(n + 1):
vis[j] = False
dfs(i, 0)
print(min(dist[i] for i in range(1, n + 1)))
if __name__ == '__main__':
dist = [0 for i in range(1001)]
vis = [False for i in range(1001)]
Adj = [[] for i in range(1001)]
N = 6
arr = [ [ 1, 4 ], [ 2, 3 ],
[ 3, 4 ], [ 4, 5 ], [ 5, 6 ] ]
minFarthestDistance(arr, N)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int[] dist;
static bool[] vis;
static void dfs(int u, List<List<int>> Adj, int s)
{
vis[u] = true;
foreach(int it in Adj[u])
{
if (vis[it] == false)
{
dfs(it, Adj, s + 1);
}
}
dist[u] = Math.Max(dist[u], s);
}
static void minFarthestDistance(int[,] arr, int n)
{
dist = new int[n + 1];
Array.Fill(dist, 0);
List<List<int>> Adj = new List<List<int>>();
for(int i = 0; i < n + 1; i++)
{
Adj.Add(new List<int>());
}
for(int i = 0; i < n - 1; i++)
{
Adj[arr[i, 0]].Add(arr[i, 1]);
Adj[arr[i, 1]].Add(arr[i, 0]);
}
for(int i = 1; i <= n; i++)
{
vis = new bool[n + 1];
Array.Fill(vis, false);
dfs(i, Adj, 0);
}
int min = Int32.MaxValue;
for(int i = 1; i < dist.Length; i++)
{
if (dist[i] < min)
{
min = dist[i];
}
}
Console.WriteLine(min);
}
static public void Main ()
{
int N = 6;
int[,] arr = { { 1, 4 }, { 2, 3 },{ 3, 4 },
{ 4, 5 }, { 5, 6 } };
minFarthestDistance(arr, N);
}
}
|
Javascript
<script>
let dist=[];
let vis=[];
function dfs(u,Adj,s)
{
vis[u] = true;
for (let it=0;it<Adj[u].length;it++)
{
if (vis[Adj[u][it]] == false)
{
dfs(Adj[u][it], Adj, s + 1);
}
}
dist[u] = Math.max(dist[u], s);
}
function minFarthestDistance(arr,n)
{
dist = new Array(n + 1);
for(let i=0;i<(n+1);i++)
{
dist[i]=0;
}
let Adj = new Array(n + 1);
for(let i = 0; i < n + 1; i++)
{
Adj[i] = [];
}
for(let i = 0; i < n - 1; i++)
{
Adj[arr[i][0]].push(arr[i][1]);
Adj[arr[i][1]].push(arr[i][0]);
}
for(let i = 1; i <= n; i++)
{
vis = new Array(n + 1);
for(let i=0;i<(n+1);i++)
{
vis[i]=false;
}
dfs(i, Adj, 0);
}
let min = Number.MAX_VALUE;
for(let i = 1; i < dist.length; i++)
{
if (dist[i] < min)
min = dist[i];
}
document.write(min);
}
let N = 6;
let arr=[[ 1, 4 ], [ 2, 3 ],
[ 3, 4 ], [ 4, 5 ],
[ 5, 6 ]];
minFarthestDistance(arr, N);
</script>
|
Time Complexity: O(V*(V+E)), where V is the number of vertices and E is the number of edges.
Auxiliary Space: O(V + E)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...