Minimum sum possible of any bracket sequence of length N

Given a number N representing the length of a bracket sequence consisting of brackets ‘(‘, ‘)’. The actual sequence is not known beforehand. Given the values of both brackets ‘(‘ and ‘)’ if placed at index 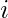$i$ in the expression.

The task is to find the minimum sum possible of any bracket sequence of length N using the above information.

Here adj[i][0] represents the value assigned to ‘)’ bracket at ith index and adj[i][1] represents the value assigned to ‘(‘ bracket at ith index.

Constraints:

There should be N/2 pairs made of brackets. That is, N/2 pairs of ‘(‘, ‘)’.
Find minimum sum of proper bracket expression.
Index starts from 0.

Examples:

Input : N = 4 
        adj[N][2] ={{5000, 3000},
                    {6000, 2000}, 
                    {8000, 1000}, 
                    {9000, 6000}} 
Output : 19000
Assigning first index as '(' for proper 
bracket expression is (_ _ _  . 
Now all the possible bracket expressions are ()() and (()). 
where '(' denotes as adj[i][1] and ')' denotes as adj[i][0]. 
Hence, for ()() sum is 3000+6000+1000+9000=19000.
and (()), sum is 3000+2000+8000+9000=220000. 
Thus answer is 19000

Input : N = 4 
        adj[N][2] = {{435, 111},
                     {43, 33}, 
                     {1241, 1111}, 
                     {234, 22}}
Output : 1499

Recommended: Please try your approach on {IDE} first, before moving on to the solution.

Algorithm:

The first element of the bracket sequence can only be ‘(‘, hence value of adj[0][1] is only of use at index 0.
Call a function to find a proper bracket expression using dp as discussed in this article.
Denote ‘(‘ as adj[i][1] and ‘)’ as a adj[i][0].
Find the minimum sum of all possible correct bracket expressions.
Return the answer + adj[0][1].

Below is the implementation of the above approach:

C++

// C++ program to find the Minimum sum possible 
// of any bracket sequence of length N using 
// the given values for brackets 
  
#include <bits/stdc++.h> 
using namespace std; 
  
#define MAX_VAL 10000000 
  
// DP array 
int dp[100][100]; 
  
// Recusive function to check for 
// correct bracket expression 
int find(int index, int openbrk, int n, int adj[][2]) 
{ 
    /// Not a proper bracket expression 
    if (openbrk < 0) 
        return MAX_VAL; 
  
    // If reaches at end 
    if (index == n) { 
  
        /// If proper bracket expression 
        if (openbrk == 0) { 
            return 0; 
        } 
        else // if not, return max 
            return MAX_VAL; 
    } 
  
    // If alreaddy visited 
    if (dp[index][openbrk] != -1) 
        return dp[index][openbrk]; 
  
    // To find out minimum sum 
    dp[index][openbrk] = min(adj[index][1] + find(index + 1, 
                                                  openbrk + 1, n, adj), 
                             adj[index][0] + find(index + 1, 
                                                  openbrk - 1, n, adj)); 
  
    return dp[index][openbrk]; 
} 
  
// Driver Code 
int main() 
{ 
    int n = 4; 
    int adj[n][2] = { { 5000, 3000 }, 
                      { 6000, 2000 }, 
                      { 8000, 1000 }, 
                      { 9000, 6000 } }; 
  
    memset(dp, -1, sizeof(dp)); 
  
    cout << find(1, 1, n, adj) + adj[0][1] << endl; 
  
    return 0; 
} 

Java

// Java program to find the Minimum sum possible  
// of any bracket sequence of length N using  
// the given values for brackets  
  
public class GFG { 
  
    final static int MAX_VAL = 10000000 ; 
  
    // DP array 
    static int dp[][] = new int[100][100]; 
  
    // Recursive function to check for 
    // correct bracket expression 
    static int find(int index, int openbrk, int n, int adj[][]) 
    { 
        /// Not a proper bracket expression 
        if (openbrk < 0) 
            return MAX_VAL; 
  
        // If reaches at end 
        if (index == n) { 
  
            /// If proper bracket expression 
            if (openbrk == 0) { 
                return 0; 
            } 
            else // if not, return max 
                return MAX_VAL; 
        } 
  
        // If alreaddy visited 
        if (dp[index][openbrk] != -1) 
            return dp[index][openbrk]; 
  
        // To find out minimum sum 
        dp[index][openbrk] = Math.min(adj[index][1] + find(index + 1, 
                                                      openbrk + 1, n, adj), 
                                 adj[index][0] + find(index + 1, 
                                                      openbrk - 1, n, adj)); 
  
        return dp[index][openbrk]; 
    } 
  
  
// Driver code 
    public static void main(String args[]) 
    { 
            int n = 4; 
            int adj[][] = { { 5000, 3000 }, 
                              { 6000, 2000 }, 
                              { 8000, 1000 }, 
                              { 9000, 6000 } }; 
  
            for (int i = 0; i < dp.length; i ++) 
                for (int j = 0; j < dp.length; j++) 
                    dp[i][j] = -1 ; 
                  
  
            System.out.println(find(1, 1, n, adj) + adj[0][1]); 
  
  
    } 
    // This code is contributed by ANKITRAI1 
} 

Python3

# Python 3 program to find the Minimum sum  
# possible of any bracket sequence of length 
# N using the given values for brackets 
  
MAX_VAL = 10000000
  
# DP array 
dp = [[-1 for i in range(100)] 
          for i in range(100)] 
  
# Recusive function to check for 
# correct bracket expression 
def find(index, openbrk, n, adj): 
      
    # Not a proper bracket expression 
    if (openbrk < 0): 
        return MAX_VAL 
  
    # If reaches at end 
    if (index == n): 
          
        # If proper bracket expression 
        if (openbrk == 0): 
            return 0
              
    # if not, return max 
        else: 
            return MAX_VAL 
  
    # If alreaddy visited 
    if (dp[index][openbrk] != -1): 
        return dp[index][openbrk] 
  
    # To find out minimum sum 
    dp[index][openbrk] = min(adj[index][1] + find(index + 1,  
                                             openbrk + 1, n, adj),  
                             adj[index][0] + find(index + 1,  
                                             openbrk - 1, n, adj)) 
  
    return dp[index][openbrk] 
  
# Driver Code 
if __name__ == '__main__': 
    n = 4; 
    adj = [[5000, 3000],[6000, 2000], 
           [8000, 1000],[9000, 6000]] 
  
    print(find(1, 1, n, adj) + adj[0][1]) 
      
# This code is contributed by 
# Sanjit_Prasad 

C#

// C# program to find the Minimum sum possible  
// of any bracket sequence of length N using  
// the given values for brackets  
using System;  
    
class GFG  
{  
    public static int MAX_VAL = 10000000; 
      
    // DP array  
    public static int[,] dp = new int[100,100];  
        
    // Recusive function to check for  
    // correct bracket expression  
    public static int find(int index, int openbrk, int n, int[,] adj)  
    {  
        /// Not a proper bracket expression  
        if (openbrk < 0)  
            return MAX_VAL;  
        
        // If reaches at end  
        if (index == n) {  
        
            /// If proper bracket expression  
            if (openbrk == 0) {  
                return 0;  
            }  
            else // if not, return max  
                return MAX_VAL;  
        }  
        
        // If alreaddy visited  
        if (dp[index,openbrk] != -1)  
            return dp[index,openbrk];  
        
        // To find out minimum sum  
        dp[index,openbrk] = Math.Min(adj[index,1] + find(index + 1,  
                                                      openbrk + 1, n, adj),  
                                 adj[index,0] + find(index + 1,  
                                                      openbrk - 1, n, adj));  
        
        return dp[index,openbrk];  
    }  
        
    // Driver Code       
      
    static void Main()  
    {  
        int n = 4; 
           
        int[,] adj = new int[,]{  
                            { 5000, 3000 },  
                            { 6000, 2000 },  
                            { 8000, 1000 },  
                            { 9000, 6000 }  
        };  
        
        for(int i = 0; i < 100; i++) 
            for(int j = 0; j < 100; j++) 
                dp[i,j] = -1; 
        
        Console.Write(find(1, 1, n, adj) + adj[0,1] + "\n");  
    } 
    //This code is contributed by DrRoot_ 
} 

PHP

<?php 
// PHP program to find the Minimum sum possible 
// of any bracket sequence of length N using 
// the given values for brackets 
$MAX_VAL = 10000000; 
$dp = array_fill(0, 100,  
      array_fill(0, 100, -1)); 
  
// Recusive function to check for 
// correct bracket expression 
function find($index, $openbrk, $n, $adj) 
{ 
    global $MAX_VAL; 
    global $dp; 
      
    /// Not a proper bracket expression 
    if ($openbrk < 0) 
        return $MAX_VAL; 
  
    // If reaches at end 
    if ($index == $n)  
    { 
  
        /// If proper bracket expression 
        if ($openbrk == 0)  
        { 
            return 0; 
        } 
        else // if not, return max 
            return $MAX_VAL; 
    } 
  
    // If alreaddy visited 
    if ($dp[$index][$openbrk] != -1) 
        return $dp[$index][$openbrk]; 
  
    // To find out minimum sum 
    $dp[$index][$openbrk] = min($adj[$index][1] +  
                           find($index + 1, $openbrk + 1, $n, $adj),  
                                $adj[$index][0] +  
                           find($index + 1, $openbrk - 1, $n, $adj)); 
  
    return $dp[$index][$openbrk]; 
} 
  
// Driver Code 
$n = 4; 
$adj = array(array(5000, 3000), 
             array(6000, 2000), 
             array(8000, 1000), 
             array(9000, 6000)); 
  
echo find(1, 1, $n, $adj) + $adj[0][1]; 
  
// This code is contributed by ihritik 
?> 

Output:

Time Complexity: O(N²)

My Personal Notes

Recommended: Please try your approach on {IDE} first, before moving on to the solution.

C++

Java

Python3

C#

PHP

Recommended Posts: