Minimum sum falling path in a NxN grid
Last Updated :
20 Feb, 2023
Given a square array A of integers of size NxN. The task is to find the minimum sum of a falling path through A.
A falling path will start at any element in the first row and ends in last row. It chooses one element from each next row. The next row’s choice must be in a column that is different from the previous row’s column by at most one.
Examples:
Input: N = 2
mat[2][2] = {{5, 10},{25, 15}}
Output: 20
Selected elements are 5, 15.
Input: N = 3
mat[3][3] ={{1, 2, 3}, { 4, 5, 6}, { 7, 8, 9}}
Output: 12
Selected elements are 1, 4, 7.
Approach: This problem has an optimal substructure, meaning that the solutions to sub-problems can be used to solve larger instances of this problem. This makes dynamic programming came into existence.
Let dp[R][C] be the minimum total weight of a falling path starting at [R, C] in first row and reaching to the bottom row of A.
Then, ![Rendered by QuickLaTeX.com dp[R][C] = A[R][C] + min(dp[R+1, C-1], dp[R+1, C], dp[R+1, C+1])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-568fdda41144f037821bb01972718063_l3.png) , and the answer is minimum value of first row i:e
, and the answer is minimum value of first row i:e 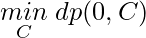 .
.
We would make an auxiliary array dp to cache intermediate values dp[R][C]. However, we will use A to cache these values. Our goal is to transform the values of A into the values of dp.
We begins processing each row, starting with the second last row. We set ![Rendered by QuickLaTeX.com A[R][C] = min(A[R+1, C-1], A[R+1, C], A[R+1, C+1])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7d226a562fe1785b7359ede25d0d6c45_l3.png) , handling boundary conditions gracefully.
, handling boundary conditions gracefully.
Explanation of above Approach:
Let’s look at the recursion a little more to get a handle on why it works. For an array like A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]], imagine you are at (1, 0) (A[1][0] = 4). You can either go to (2, 0) and get a weight of 7, or (2, 1) and get a weight of 8. Since 7 is lower, we say that the minimum total weight at (1, 0) is dp(1, 0) = 5 + 7 (7 for the original A[R][C].)
After visiting (1, 0), (1, 1), and (1, 2), A [which is storing the values of our dp], looks like [[1, 2, 3], [11, 12, 14], [7, 8, 9]]. We do this procedure again by visiting (0, 0), (0, 1), (0, 2).
We get 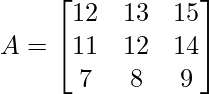 , and the final answer is min(A[0][C]) = 12 for all C in range 0 to n.
, and the final answer is min(A[0][C]) = 12 for all C in range 0 to n.
Below is the implementation of above approach.
C++
#include <bits/stdc++.h>
using namespace std;
const int n = 3;
int minFallingPathSum(int (&A)[n][n])
{
for (int R = n - 2; R >= 0; --R) {
for (int C = 0; C < n; ++C) {
int best = A[R + 1][C];
if (C > 0)
best = min(best, A[R + 1][C - 1]);
if (C + 1 < n)
best = min(best, A[R + 1][C + 1]);
A[R][C] = A[R][C] + best;
}
}
int ans = INT_MAX;
for (int i = 0; i < n; ++i)
ans = min(ans, A[0][i]);
return ans;
}
int main()
{
int A[n][n] = { { 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 } };
cout << minFallingPathSum(A);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int n = 3;
static int minFallingPathSum(int A[][])
{
for (int R = n - 2; R >= 0; --R) {
for (int C = 0; C < n; ++C) {
int best = A[R + 1][C];
if (C > 0)
best = Math.min(best, A[R + 1][C - 1]);
if (C + 1 < n)
best = Math.min(best, A[R + 1][C + 1]);
A[R][C] = A[R][C] + best;
}
}
int ans = Integer.MAX_VALUE;
for (int i = 0; i < n; ++i)
ans = Math.min(ans, A[0][i]);
return ans;
}
public static void main (String[] args) {
int A[][] = { { 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 } };
System.out.println( minFallingPathSum(A));
}
}
|
Python 3
import sys
n = 3
def minFallingPathSum(A) :
for R in range(n - 2, -1, -1) :
for C in range(n) :
best = A[R + 1][C]
if C > 0 :
best = min(best, A[R + 1][C - 1])
if C + 1 < n :
best = min(best, A[R + 1][C + 1])
A[R][C] = A[R][C] + best
ans = sys.maxsize
for i in range(n) :
ans = min(ans, A[0][i])
return ans
if __name__ == "__main__" :
A = [ [ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9] ]
print(minFallingPathSum(A))
|
C#
using System;
class GFG {
static int n = 3;
static int minFallingPathSum(int[,] A)
{
for (int R = n - 2; R >= 0; --R) {
for (int C = 0; C < n; ++C) {
int best = A[R + 1,C];
if (C > 0)
best = Math.Min(best, A[R + 1,C - 1]);
if (C + 1 < n)
best = Math.Min(best, A[R + 1,C + 1]);
A[R,C] = A[R,C] + best;
}
}
int ans = int.MaxValue;
for (int i = 0; i < n; ++i)
ans = Math.Min(ans, A[0,i]);
return ans;
}
public static void Main () {
int[,] A = { { 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 } };
Console.WriteLine( minFallingPathSum(A));
}
}
|
Javascript
const n = 3;
function minFallingPathSum(A) {
for (let R = n - 2; R >= 0; --R) {
for (let C = 0; C < n; ++C) {
let best = A[R + 1][C];
if (C > 0)
best = Math.min(best, A[R + 1][C - 1]);
if (C + 1 < n)
best = Math.min(best, A[R + 1][C + 1]);
A[R][C] = A[R][C] + best;
}
}
let ans = Number.MAX_SAFE_INTEGER;
for (let i = 0; i < n; ++i)
ans = Math.min(ans, A[0][i]);
return ans;
}
function main() {
let A = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ];
console.log(minFallingPathSum(A));
}
main();
|
Time Complexity: O(N2)
Top-Down Approach:
- Compute a function and follow up the recursive solution.
- Consider all the base conditions.
- Start moving in all the possible directions as mentioned in the question.
- When reached the end corner of the grid, simply consider the minimum fall path sum.
- Return the minimum falling path sum.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
const int n = 3;
int helper(int i, int j, int A[n][n],vector<vector<int>>&dp){
if(j<0 || j>=n)
return 1e9;
if(i==0)
return A[0][j];
if(dp[i][j]!=-1)
return dp[i][j];
int a = A[i][j] + helper(i-1,j,A,dp);
int b = A[i][j] + helper(i-1,j-1,A,dp);
int c = A[i][j] + helper(i-1,j+1,A,dp);
return dp[i][j] = min(a,min(b,c));
}
int minFallingPathSum(int A[n][n]) {
vector<vector<int>> dp(n,vector<int>(n,-1));
int res=1e9;
for(int k=0;k<n;k++){
res=min(res,helper(n-1,k,A,dp)) ;
}
return res;
}
int main()
{
int A[n][n] = { { 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 } };
cout << minFallingPathSum(A);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int n = 3;
public static int minFallingPathSum(int[][] matrix) {
int rows = matrix.length;
int columns = matrix[0].length;
Integer[][] dp = new Integer[rows][columns];
int ans = Integer.MAX_VALUE;
for(int column = 0; column < columns; column += 1) {
ans = Math.min(ans, minPathSum(rows - 1, column, matrix, dp));
}
return ans;
}
private static int minPathSum(int row, int column, int[][] matrix, Integer[][] dp) {
if(row < 0) {
return 0;
}
if(column < 0 || column >= matrix[0].length) {
return 100000000;
}
if(dp[row][column] != null) {
return dp[row][column];
}
int ans = matrix[row][column] + Math.min(minPathSum(row - 1, column - 1, matrix, dp), Math.min(minPathSum(row - 1, column, matrix, dp), minPathSum(row - 1, column + 1, matrix, dp)));
return dp[row][column] = ans;
}
public static void main (String[] args) {
int A[][] = { { 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 } };
System.out.println( minFallingPathSum(A));
}
}
|
Python3
def fallingpathsum(grid, row, col, Row, Col, dp):
if row == Row-1 and col == Col-1:
return grid[row][col]
if row > Row-1 or col > Col-1:
return 0
rightdown = fallingpathsum(grid, row+1, col, Row, Col, dp)
rdd = fallingpathsum(grid, row+1, col+1, Row, Col, dp)
ldd = fallingpathsum(grid, row+1, col-1, Row, Col, dp)
if dp[row][col] == -1:
dp[row][col] = grid[row][col] + min(rightdown, ldd, rdd)
return dp[row][col]
grid = [[1,2,3], [4,5,6],[7,8,9]]
Row = len(grid)
Col = len(grid[0])
dp = [[-1 for i in range(Row)]for _ in range(Col)]
print(fallingpathsum(grid, 0, 0, Row, Col, dp))
|
C#
using System;
using System.Collections.Generic;
class GFG {
static int n = 3;
public static int minFallingPathSum(int[][] matrix)
{
int rows = matrix.Length;
int columns = matrix[0].Length;
int[][] dp = new int[rows][];
for (int i = 0; i < dp.Length; i++)
dp[i] = new int[columns];
int ans = int.MaxValue;
for (int column = 0; column < columns;
column += 1) {
ans = Math.Min(ans, minPathSum(rows - 1, column,
matrix, dp));
}
return ans;
}
private static int minPathSum(int row, int column,
int[][] matrix,
int[][] dp)
{
if (row < 0) {
return 0;
}
if (column < 0 || column >= matrix[0].Length) {
return 100000000;
}
if (dp[row][column] != 0) {
return dp[row][column];
}
int ans
= matrix[row][column]
+ Math.Min(
minPathSum(row - 1, column - 1, matrix,
dp),
Math.Min(minPathSum(row - 1, column,
matrix, dp),
minPathSum(row - 1, column + 1,
matrix, dp)));
return dp[row][column] = ans;
}
public static void Main(string[] args)
{
int[][] A = { new int[] { 1, 2, 3 },
new int[] { 4, 5, 6 },
new int[] { 7, 8, 9 } };
Console.WriteLine(minFallingPathSum(A));
}
}
|
Javascript
const n = 3;
function helper(i, j, A, dp) {
if (j < 0 || j >= n) {
return Number.MAX_SAFE_INTEGER;
}
if (i == 0) {
return A[0][j];
}
if (dp[i][j] != -1) {
return dp[i][j];
}
let a = A[i][j] + helper(i-1, j, A, dp);
let b = A[i][j] + helper(i-1, j-1, A, dp);
let c = A[i][j] + helper(i-1, j+1, A, dp);
return dp[i][j] = Math.min(a, Math.min(b, c));
}
function minFallingPathSum(A) {
let dp = Array.from(Array(n), () => Array(n).fill(-1));
let res = Number.MAX_SAFE_INTEGER;
for (let k = 0; k < n; k++) {
res = Math.min(res, helper(n-1, k, A, dp));
}
return res;
}
let A = [ [1, 2, 3],
[4, 5, 6],
[7, 8, 9]
];
console.log(minFallingPathSum(A));
|
Complexity Analysis:
- Time Complexity: O(N2)
- Space Complexity: O(N2)+O(N)
Bottom-up Approach:
- Initialize a 2D dp array of size NxN with all values set to zero.
- Iterate over the grid from bottom to top and for each cell, calculate the minimum sum from the three possible paths from the cells below it.
- For each cell (i,j), update the value in the dp array as follows:
dp[i][j] = grid[i][j] + min(dp[i+1][j], dp[i+1][j-1], dp[i+1][j+1]) - For the first row (i=0), we will not have any cells below, so the value of the cell is equal to the grid value.
- After iterating over the entire grid, the minimum sum is the minimum value in the first row of the dp array.
- Return the minimum sum.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
const int n = 3;
int minFallingPathSum(int A[n][n])
{
int ans = 0;
vector<vector<int> > dp(n, vector<int>(n, 0));
for (int i = 0; i < n; i++) {
int minimum = INT_MAX;
for (int j = 0; j < n; j++) {
if (i == 0) {
dp[i][j] = A[i][j];
minimum = min(minimum, dp[i][j]);
continue;
}
int up = A[i][j];
int left = A[i][j], right = A[i][j];
up += dp[i - 1][j];
if (j > 0) {
left += dp[i - 1][j - 1];
}
else {
left = INT_MAX;
}
if (j < n - 1) {
right += dp[i - 1][j + 1];
}
else {
right = INT_MAX;
}
dp[i][j] += min(left, min(right, up));
minimum = min(minimum, dp[i][j]);
}
ans = minimum;
}
return ans;
}
int main()
{
int A[n][n] = { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
cout << minFallingPathSum(A);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int n = 3;
static int minFallingPathSum(int A[][])
{
if (A == null || A.length == 0 || A[0].length == 0)
return 0;
int m = A.length;
int n = A[0].length;
int[][] M = new int[m][n];
for (int j = 0; j < n; j++) {
M[0][j] = A[0][j];
}
for (int i = 1; i < m; i++) {
for (int j = 0; j < n; j++) {
if (j == 0) {
M[i][j] = Math.min(M[i - 1][j],
M[i - 1][j + 1]);
}
else if (j == n - 1) {
M[i][j] = Math.min(M[i - 1][j - 1],
M[i - 1][j]);
}
else {
M[i][j] = Math.min(M[i - 1][j - 1],
M[i - 1][j]);
M[i][j] = Math.min(M[i][j],
M[i - 1][j + 1]);
}
M[i][j] += A[i][j];
}
}
int min = Integer.MAX_VALUE;
for (int num : M[m - 1]) {
min = Math.min(min, num);
}
return min;
}
public static void main(String[] args)
{
int A[][]
= { { 1, 2, 3 }, { 4, 5, 6 }, { 7, 8, 9 } };
System.out.println(minFallingPathSum(A));
}
}
|
C#
using System;
class GFG {
static int n = 3;
static int MinFallingPathSum(int[][] A)
{
if (A == null || A.Length == 0 || A[0].Length == 0)
return 0;
int m = A.Length;
int n = A[0].Length;
int[][] M = new int[m][];
for (int i = 0; i < m; i++) {
M[i] = new int[n];
}
for (int j = 0; j < n; j++) {
M[0][j] = A[0][j];
}
for (int i = 1; i < m; i++) {
for (int j = 0; j < n; j++) {
if (j == 0) {
M[i][j] = Math.Min(M[i - 1][j],
M[i - 1][j + 1]);
}
else if (j == n - 1) {
M[i][j] = Math.Min(M[i - 1][j - 1],
M[i - 1][j]);
}
else {
M[i][j] = Math.Min(M[i - 1][j - 1],
M[i - 1][j]);
M[i][j] = Math.Min(M[i][j],
M[i - 1][j + 1]);
}
M[i][j] += A[i][j];
}
}
int min = int.MaxValue;
foreach (int num in M[m - 1]) {
min = Math.Min(min, num);
}
return min;
}
static void Main(string[] args)
{
int[][] A = new int[][] { new int[] { 1, 2, 3 },
new int[] { 4, 5, 6 },
new int[] { 7, 8, 9 } };
Console.WriteLine(MinFallingPathSum(A));
}
}
|
Javascript
const n = 3;
function minFallingPathSum(A) {
let dp = Array.from(Array(n), () => Array(n).fill(0));
for (let i = 0; i < n; i++) {
dp[0][i] = A[0][i];
}
for (let i = 1; i < n; i++) {
for (let j = 0; j < n; j++) {
let a = (j > 0) ? dp[i - 1][j - 1] : Number.MAX_SAFE_INTEGER;
let b = dp[i - 1][j];
let c = (j < n - 1) ? dp[i - 1][j + 1] : Number.MAX_SAFE_INTEGER;
dp[i][j] = A[i][j] + Math.min(a, Math.min(b, c));
}
}
return Math.min(...dp[n - 1]);
}
let A = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
];
console.log(minFallingPathSum(A));
|
Python3
import sys
n = 3
def minFallingPathSum(A):
ans = 0
dp = [[0 for i in range(n)] for j in range(n)]
for i in range(n):
minimum = sys.maxsize
for j in range(n):
if i == 0:
dp[i][j] = A[i][j]
minimum = min(minimum, dp[i][j])
continue
up = A[i][j]
left = A[i][j]
right = A[i][j]
up += dp[i-1][j]
if j > 0:
left += dp[i-1][j-1]
else:
left = sys.maxsize
if j < n - 1:
right += dp[i-1][j+1]
else:
right = sys.maxsize
dp[i][j] += min(left, min(right, up))
minimum = min(minimum, dp[i][j])
ans = minimum
return ans
A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
print(minFallingPathSum(A))
|
Complexity Analysis:
- Time Complexity: O(N2)
- Space Complexity: O(N2)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...