Minimum size binary string required such that probability of deleting two 1’s at random is 1/X

Given a value X, the task is to find a minimum size binary string, such that if any 2 characters are deleted at random, the probability that both the characters will be ‘1’ is 1/X. Print the size of such binary string.

Example:

Input: X = 2 
Output: 4 
Explanation:
Let the binary string be “0111”. 
Probability of choosing 2 1s from given string is = 3C2 / 4C2 = 3/6 = 1/2 (which is equal to 1/X). 
Hence, the required size is 4. 
(Any 4 size binary string with 3 ‘1’s and 1 ‘0’ can be taken for this example).
Input: X = 8 
Output: 5 

Approach: We will try to find a formula to solve this problem.  

Let 
r = Number of 1’s in the string 
and 
b = Number of 0’s in the string.

• If two characters are deleted at random, then 

 Total number of ways = (r + b) _{C 2.}

• If 2 characters are desired to be 1’s, Favourable number of cases = r _{C 2}. 
  
• Hence, P(both are 1’s) = r_C2 / (r + b)_C2. 
  
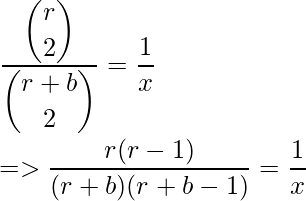
• A tricky observation to further proceed our calculation is: 
  
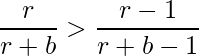
• Squaring the inequality and comparing with the equality, we get 
  
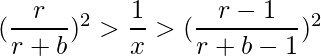
• If r > 1, we take square root on all 3 sides. 
  
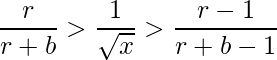
• Taking the leftmost part of the inequality, we get:  
  
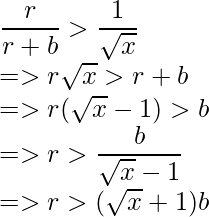
• Similarly, taking the rightmost part of the inequality, we get:  
  
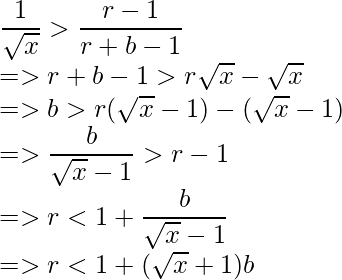
• Combining the derived conclusions, we get the range of r in terms of b.  
  
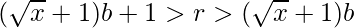
• For the minimum value of string, we set b = 1
  
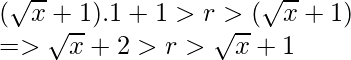
• In order to get a valid minimum r, we take the first integer value of r in this range.

For Example: if X = 2

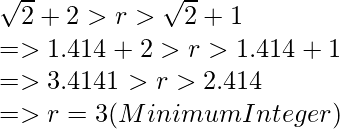
Hence, r = 3 and b = 1. 
P(both character are 1’s) = 3C2 / 4C2 = 2/4 = 1/2 

Below is the implementation of the above approach.

C++

// C++ implementation of the
// above approach

#include <bits/stdc++.h>
using namespace std;

// Function returns the minimum
// size of the string
int MinimumString(int x)
{
    // From formula
    int b = 1;

    // Left limit of r
    double left_lim = sqrt(x) + 1.0;

    // Right limit of r
    double right_lim = sqrt(x) + 2.0;

    int r;
    for (int i = left_lim; i <= right_lim; i++) {
        if (i > left_lim and i < right_lim) {
            // Smallest integer in
            // the valid range
            r = i;
            break;
        }
    }

    return b + r;
}

// Driver Code
int main()
{

    int X = 2;
    cout << MinimumString(X);
    return 0;
}

Java

// Java implementation of the
// above approach
import java.util.*;

class GFG{

// Function returns the minimum
// size of the String
static int MinimumString(int x)
{

    // From formula
    int b = 1;

    // Left limit of r
    double left_lim = Math.sqrt(x) + 1.0;

    // Right limit of r
    double right_lim = Math.sqrt(x) + 2.0;

    int r = 0;
    for(int i = (int)left_lim; i <= right_lim; i++)
    {
        if (i > left_lim && i < right_lim)
        {

            // Smallest integer in
            // the valid range
            r = i;
            break;
        }
    }
    return b + r;
}

// Driver Code
public static void main(String[] args)
{
    int X = 2;
    System.out.print(MinimumString(X));
}
}

// This code is contributed by PrinciRaj1992

Python3

# Python3 implementation of
# the above approach
from math import sqrt

# Function returns the minimum
# size of the string
def MinimumString(x):

    # From formula
    b = 1

    # Left limit of r
    left_lim = sqrt(x) + 1.0

    # Right limit of r
    right_lim = sqrt(x) + 2.0

    for i in range(int(left_lim),
                   int(right_lim) + 1):
        if(i > left_lim and i < right_lim):

            # Smallest integer in
            # the valid range
            r = i
            break

    return b + r

# Driver Code
if __name__ == '__main__':

    X = 2

    print(MinimumString(X))

# This code is contributed by Shivam Singh

C#

// C# implementation of the
// above approach
using System;

class GFG{

// Function returns the minimum
// size of the String
static int MinimumString(int x)
{

    // From formula
    int b = 1;

    // Left limit of r
    double left_lim = Math.Sqrt(x) + 1.0;

    // Right limit of r
    double right_lim = Math.Sqrt(x) + 2.0;

    int r = 0;
    for(int i = (int)left_lim; i <= right_lim; i++)
    {
        if (i > left_lim && i < right_lim)
        {

            // Smallest integer in
            // the valid range
            r = i;
            break;
        }
    }
    return b + r;
}

// Driver Code
public static void Main(String[] args)
{
    int X = 2;

    Console.Write(MinimumString(X));
}
}

// This code is contributed by gauravrajput1

Javascript

<script>

// Javascript program for
// the above approach

// Function returns the minimum
// size of the String
function MinimumString(x)
{

    // From formula
    let b = 1;

    // Left limit of r
    let left_lim = Math.sqrt(x) + 1.0;

    // Right limit of r
    let right_lim = Math.sqrt(x) + 2.0;

    let r = 0;
    for(let i = Math.floor(left_lim); i <= Math.floor(right_lim); i++)
    {
        if (i > left_lim && i < right_lim)
        {

            // Smallest integer in
            // the valid range
            r = i;
            break;
        }
    }
    return b + r;
}

// Driver Code

     let  X = 2;
    document.write(MinimumString(X));

</script>

Output:

4

Time Complexity: O(1), as the difference between left_lim and right_lim will be always less than 1. 
Auxiliary Space: O(1)