Minimum numbers needed to express every integer below N as a sum
Last Updated :
19 Jul, 2022
We have an integer N. We need to express N as a sum of K integers such that by adding some(or all) of these integers we can get all the numbers in the range[1, N]. What is the minimum value of K?
Examples:
Input : N = 7
Output : 3
Explanation : Three integers are 1, 2, 4. By adding some(or all) of these groups we can get all number in the range 1 to N.
1; 2; 1+2=3; 4; 1+4=5; 2+4=6; 1+2+4=7
Input : N = 32
Output : 6
Explanation : Six integers are 1, 2, 4, 8, 16, 1.
1st we solve the problem for small numbers by hand.
n=1 : 1
n=2 : 1, 1
n=3 : 1, 2
n=4 : 1, 2, 1
n=5 : 1, 2, 2
n=6 : 1, 2, 3
n=7 : 1, 2, 4
n=8 : 1, 2, 4, 1
If we inspect this closely we can see that if 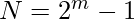 then the integers are
then the integers are ![Rendered by QuickLaTeX.com [1, 2, 4..., 2^{m-1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5b26be19db881b35e2ab87bf5cd3975d_l3.png) . Which is just another way of saying
. Which is just another way of saying 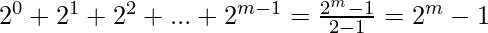 .So now we know for
.So now we know for 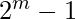 minimum value of K is m.
minimum value of K is m.
Now we inspect what happens for 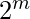 .For
.For 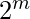 we just add a new integer 1 to our list of integers. Realize that for every number from
we just add a new integer 1 to our list of integers. Realize that for every number from 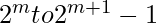 we can increase the newly added integer by 1 and that will be the optimal list of integers. To verify look at N=4 to N=7, minimum K does not change; only the last integer is increased in each step.
we can increase the newly added integer by 1 and that will be the optimal list of integers. To verify look at N=4 to N=7, minimum K does not change; only the last integer is increased in each step.
Of course we can implement this in iterative manner in O(log N) time (by inserting successive powers of 2 in the list and the last element will be of the form N-(2^n-1)). But this is exactly same as finding the length of binary expression of N which also can be done in O(log N) time.
C++
#include <bits/stdc++.h>
using namespace std;
int countBits(int n)
{
int count = 0;
while (n) {
count++;
n >>= 1;
}
return count;
}
int main()
{
int n = 32;
cout << "Minimum value of K is = "
<< countBits(n) << endl;
return 0;
}
|
Java
import java.io.*;
class GFG {
static int countBits(int n)
{
int count = 0;
while (n>0) {
count++;
n >>= 1;
}
return count;
}
public static void main (String[] args) {
int n = 32;
System.out.println("Minimum value of K is = "+
countBits(n));
}
}
|
Python3
def countBits(n):
count = 0;
while (n):
count += 1;
n >>= 1;
return count;
n = 32;
print("Minimum value of K is =",
countBits(n));
|
C#
using System;
class GFG
{
static int countBits(int n)
{
int count = 0;
while (n > 0)
{
count++;
n >>= 1;
}
return count;
}
static public void Main ()
{
int n = 32;
Console.WriteLine("Minimum value of K is = "+
countBits(n));
}
}
|
PHP
<?php
function countBits($n)
{
$count = 0;
while ($n)
{
$count++;
$n >>= 1;
}
return $count;
}
$n = 32;
echo "Minimum value of K is = ",
countBits($n), "\n";
?>
|
Javascript
<script>
function countBits(n)
{
var count = 0;
while (n)
{
count++;
n >>= 1;
}
return count;
}
var n = 32;
document.write("Minimum value of K is = " +
countBits(n));
</script>
|
output:
Minimum value of K is = 6
Time Complexity: O(log n)
Auxiliary Space: O(1)
Please see count set bits for more efficient methods to count set bits in an integer.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...