Minimum number to be added to all digits of X to make X > Y
Last Updated :
08 Mar, 2022
Given two numbers X and Y of the same length, the task is to find the minimum number d that needs to be added to all the digits of X such that it becomes larger than Y.
Examples:
Input: X = 123, Y = 222
Output: 1
Explanation:
Add 1 to all digits of X
Then X becomes {2, 3, 4} which is
lexicographically larger than {2, 2, 2}.
Input: X = 4512, Y = 2998
Output: 0
Explanation:
X is already lexicographically larger than Y
so the answer will be 0.
Approach: This problem can be solved easily by breaking it into three cases
- Case 1: Find if X is already lexicographically larger than Y. If yes, then we don’t need to do anything.
- Case 2: Otherwise add (Y[0] – X[0]) to all elements of X and then check if X is lexicographically larger than Y or not.
- Case 3: If it is still not larger, then answer will be (Y[0] – X[0]) + 1 because the first elements of X become larger than first element of Y means X[0] > Y[0].
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool IsLarger(int X[], int Y[], int n)
{
for (int i = 0; i < n; i++) {
if (X[i] < Y[i]) {
return false;
}
}
return true;
}
int solve(int X[], int Y[], int n)
{
int ans = 0;
if (IsLarger(X, Y, n)) {
ans = 0;
}
else {
int d = Y[0] - X[0];
for (int i = 0; i < n; i++) {
X[i] += d;
}
if (IsLarger(X, Y, n)) {
ans = d;
}
else {
ans = d + 1;
}
}
return ans;
}
int main()
{
int X[] = { 2, 3, 6, 9 };
int Y[] = { 3, 4, 8, 1 };
int n = sizeof(X) / sizeof(X[0]);
cout << solve(X, Y, n);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static boolean IsLarger(int[] X,
int[] Y, int n)
{
for (int i = 0; i < n; i++)
{
if (X[i] < Y[i])
{
return false;
}
}
return true;
}
static int solve(int X[], int Y[], int n)
{
int ans = 0;
if (IsLarger(X, Y, n))
ans = 0;
else
{
int d = Y[0] - X[0];
for (int i = 0; i < n; i++)
X[i] += d;
if (IsLarger(X, Y, n))
ans = d;
else
{
ans = d + 1;
}
}
return ans;
}
public static void main(String[] args)
{
int X[] = { 2, 3, 6, 9 };
int Y[] = { 3, 4, 8, 1 };
int n = X.length;
System.out.println(solve(X, Y, n));
}
}
|
Python3
def IsLarger(X, Y, n) :
for i in range(n) :
if (X[i] < Y[i]) :
return False;
return True;
def solve(X, Y, n) :
ans = 0;
if (IsLarger(X, Y, n)) :
ans = 0;
else :
d = Y[0] - X[0];
for i in range(n) :
X[i] += d;
if (IsLarger(X, Y, n)) :
ans = d;
else :
ans = d + 1;
return ans;
if __name__ == "__main__" :
X = [ 2, 3, 6, 9 ];
Y = [ 3, 4, 8, 1 ];
n = len(X);
print(solve(X, Y, n));
|
C#
using System;
class GFG
{
static bool IsLarger(int[] X,
int[] Y, int n)
{
for (int i = 0; i < n; i++)
{
if (X[i] < Y[i])
{
return false;
}
}
return true;
}
static int solve(int []X, int []Y, int n)
{
int ans = 0;
if (IsLarger(X, Y, n))
ans = 0;
else
{
int d = Y[0] - X[0];
for (int i = 0; i < n; i++)
X[i] += d;
if (IsLarger(X, Y, n))
ans = d;
else
{
ans = d + 1;
}
}
return ans;
}
public static void Main(String[] args)
{
int []X = { 2, 3, 6, 9 };
int []Y = { 3, 4, 8, 1 };
int n = X.Length;
Console.WriteLine(solve(X, Y, n));
}
}
|
Javascript
<script>
function IsLarger(X, Y, n)
{
for (let i = 0; i < n; i++) {
if (X[i] < Y[i]) {
return false;
}
}
return true;
}
function solve(X, Y, n)
{
let ans = 0;
if (IsLarger(X, Y, n)) {
ans = 0;
}
else {
let d = Y[0] - X[0];
for (let i = 0; i < n; i++) {
X[i] += d;
}
if (IsLarger(X, Y, n)) {
ans = d;
}
else {
ans = d + 1;
}
}
return ans;
}
let X = [ 2, 3, 6, 9 ];
let Y = [ 3, 4, 8, 1 ];
let n = X.length;
document.write(solve(X, Y, n));
</script>
|
Time Complexity: 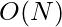 , where N is the length of X or Y
, where N is the length of X or Y
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...