Minimum number of moves required to reach the destination by the king in a chess board

Given four integers sourceX, sourceY, destinationX and destinationY which represent the source and destination coordinates on a chessboard. The task is to find the minimum number of moves required by the king to reach from source to destination. 
A king can move to the square that has a common side or a common vertex with the square the king is currently in (generally there are 8 different squares he can move to).

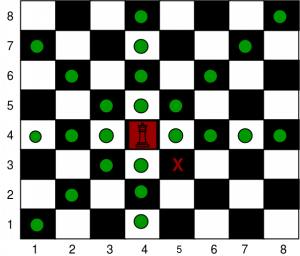
Print path using L, R, U, D, LU, LD, RU and RD where L, R, U and D represent left, right, up and down respectively.

Examples:

Input: sourceX = 4, sourceY = 4, destinationX = 3, destinationY = 5 
Output: 1 
DR

Input: sourceX = 4, sourceY = 4, destinationX = 7, destinationY = 0 
Output: 4 
UL 
UL 
UL 
L 

Approach: Move in the diagonal direction towards the destination until the king reaches same column or same row as the destination, then move towards the destination in a straight line.

Below is the implementation of the above approach: 

C++

// C++ program to Find the minimum number of moves required to
// reach the destination by the king in a chess board
#include <bits/stdc++.h>
using namespace std;

// function to Find the minimum number of moves required to
// reach the destination by the king in a chess board
void MinSteps(int SourceX, int SourceY, int DestX, int DestY)
{
    // minimum number of steps
    cout << max(abs(SourceX - DestX), abs(SourceY - DestY)) << endl;

    // while the king is not in the same row or column
    // as the destination
    while ((SourceX != DestX) || (SourceY != DestY)) {

        // Go up
        if (SourceX < DestX) {
            cout << 'U';
            SourceX++;
        }

        // Go down
        if (SourceX > DestX) {
            cout << 'D';
            SourceX--;
        }

        // Go left
        if (SourceY > DestY) {
            cout << 'L';
            SourceY--;
        }

        // Go right
        if (SourceY < DestY) {
            cout << 'R';
            SourceY++;
        }

        cout << endl;
    }
}

// Driver code
int main()
{
    int sourceX = 4, sourceY = 4;
    int destinationX = 7, destinationY = 0;

    MinSteps(sourceX, sourceY, destinationX, destinationY);

    return 0;
}

Java

// Java program to Find the minimum
// number of moves required to reach
// the destination by the king in a
// chess board
import java.io.*;

class GFG
{

// function to Find the minimum number
// of moves required to reach the
// destination by the king in a chess board
static void MinSteps(int SourceX, int SourceY,
                     int DestX, int DestY)
{
    // minimum number of steps
    System.out.println(Math.max(Math.abs(SourceX - DestX),
                     Math.abs(SourceY - DestY)));

    // while the king is not in the same
    // row or column as the destination
    while ((SourceX != DestX) ||
           (SourceY != DestY))
    {

        // Go up
        if (SourceX < DestX)
        {
            System.out.print( 'U');
            SourceX++;
        }

        // Go down
        if (SourceX > DestX)
        {
            System.out.println( 'D');
            SourceX--;
        }

        // Go left
        if (SourceY > DestY)
        {
            System.out.print( 'L');
            SourceY--;
        }

        // Go right
        if (SourceY < DestY)
        {
            System.out.print( 'R');
            SourceY++;
        }

        System.out.println();
    }
}

// Driver code
public static void main (String[] args)
{
    int sourceX = 4, sourceY = 4;
    int destinationX = 7, destinationY = 0;

    MinSteps(sourceX, sourceY,
             destinationX, destinationY);
}
}

// This code is contributed by inder_verma

Python3

# Python 3 program to Find the minimum number of moves required to
# reach the destination by the king in a chess board

# function to Find the minimum number of moves required to
# reach the destination by the king in a chess board
def MinSteps(SourceX, SourceY, DestX, DestY):
    # minimum number of steps
    print(max(abs(SourceX - DestX), abs(SourceY - DestY)))

    # while the king is not in the same row or column
    # as the destination
    while ((SourceX != DestX) or (SourceY != DestY)):
        # Go up
        if (SourceX < DestX):
            print('U',end = "")
            SourceX += 1

        # Go down
        if (SourceX > DestX):
            print('D',end = "")
            SourceX -= 1

        # Go left
        if (SourceY > DestY):
            print('L')
            SourceY -= 1

        # Go right
        if (SourceY < DestY):
            print('R',end = "")
            SourceY += 1


# Driver code
if __name__ == '__main__':
    sourceX = 4
    sourceY = 4
    destinationX = 7
    destinationY = 0

    MinSteps(sourceX, sourceY, destinationX, destinationY)

# This code is contributed by
# Surendra_Gangwar

C#

// C# program to Find the minimum
// number of moves required to reach
// the destination by the king in a
// chess board
using System;

class GFG
{

// function to Find the minimum number
// of moves required to reach the
// destination by the king in a chess board
static void MinSteps(int SourceX, int SourceY,
                     int DestX, int DestY)
{
    // minimum number of steps
    Console.WriteLine(Math.Max(Math.Abs(SourceX - DestX),
                               Math.Abs(SourceY - DestY)));

    // while the king is not in the same
    // row or column as the destination
    while ((SourceX != DestX) ||
           (SourceY != DestY))
    {

        // Go up
        if (SourceX < DestX)
        {
            Console.Write( 'U');
            SourceX++;
        }

        // Go down
        if (SourceX > DestX)
        {
            Console.Write( 'D');
            SourceX--;
        }

        // Go left
        if (SourceY > DestY)
        {
            Console.Write( 'L');
            SourceY--;
        }

        // Go right
        if (SourceY < DestY)
        {
            Console.Write( 'R');
            SourceY++;
        }

        Console.WriteLine();
    }
}

// Driver code
public static void Main ()
{
    int sourceX = 4, sourceY = 4;
    int destinationX = 7, destinationY = 0;

    MinSteps(sourceX, sourceY,
             destinationX, destinationY);
}
}

// This code is contributed by inder_verma

PHP

<?php
// PHP program to Find the minimum
// number of moves required to
// reach the destination by the
// king in a chess board

// function to Find the minimum
// number of moves required to
// reach the destination by the
// king in a chess board
function MinSteps($SourceX, $SourceY,
                  $DestX, $DestY)
{
    // minimum number of steps
    echo max(abs($SourceX - $DestX),
             abs($SourceY - $DestY)) . "\n";

    // while the king is not in the
    // same row or column as the destination
    while (($SourceX != $DestX) ||
           ($SourceY != $DestY))
    {

        // Go up
        if ($SourceX < $DestX)
        {
            echo 'U';
            $SourceX++;
        }

        // Go down
        if ($SourceX > $DestX)
        {
            echo 'D';
            $SourceX--;
        }

        // Go left
        if ($SourceY > $DestY)
        {
            echo 'L';
            $SourceY--;
        }

        // Go right
        if ($SourceY < $DestY)
        {
            echo 'R';
            $SourceY++;
        }

        echo "\n";
    }
}

// Driver code
$sourceX = 4; $sourceY = 4;
$destinationX = 7; $destinationY = 0;

MinSteps($sourceX, $sourceY,
         $destinationX, $destinationY);

// This code is contributed
// by Akanksha Rai
?>

Javascript

<script>

// Javascript program to Find the minimum
// number of moves required to reach the
// destination by the king in a chess board

// function to Find the minimum number of
// moves required to reach the destination
// by the king in a chess board
function MinSteps(SourceX, SourceY, DestX, DestY)
{

    // Minimum number of steps
    document.write(Math.max(Math.abs(SourceX - DestX),
    Math.abs(SourceY - DestY)) + "<br>");

    // While the king is not in the same row
    // or column as the destination
    while ((SourceX != DestX) ||
           (SourceY != DestY))
    {

        // Go up
        if (SourceX < DestX)
        {
            document.write('U');
            SourceX++;
        }

        // Go down
        if (SourceX > DestX)
        {
            document.write('D');
            SourceX--;
        }

        // Go left
        if (SourceY > DestY) {
            document.write('L');
            SourceY--;
        }

        // Go right
        if (SourceY < DestY)
        {
            document.write('R');
            SourceY++;
        }
        document.write("<br>");
    }
}

// Driver code
let sourceX = 4, sourceY = 4;
let destinationX = 7, destinationY = 0;

MinSteps(sourceX, sourceY, destinationX,
         destinationY);

// This code is contributed by souravmahato348

</script>

Output:

4
UL
UL
UL
L

Time complexity: O(max(a, b)), where a = sourceX and b = sourceY

Auxiliary Space: O(1), since no extra space has been taken.