Minimum number of cuts required to make circle segments equal sized
Last Updated :
11 Jul, 2022
Given an array of 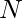 elements where each element in the array represents the degree ( 0 <= a[i] <= 359 ) at which there is already a cut in a circle. The task is to find the minimum number of additional cuts required to make circle segments equal sized.
elements where each element in the array represents the degree ( 0 <= a[i] <= 359 ) at which there is already a cut in a circle. The task is to find the minimum number of additional cuts required to make circle segments equal sized.
Examples:
Input : arr[] = { 0, 2 }
Output : 178
Input : arr[] = { 30, 60, 180 }
Output : 9
Approach : An efficient way to solve the above problem is to find gcd of all consecutive difference in angles. This gcd is the maximum angle of one circular segment and then the number of segments will be 360/gcdObtained. But, there are already N cuts. so additional cuts will be (360/gcdObtained) – N.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minimumCuts(int a[], int n)
{
sort(a, a + n);
int gcd = a[1] - a[0];
int s = gcd;
for (int i = 2; i < n; i++) {
gcd = __gcd(gcd, a[i] - a[i - 1]);
s += a[i] - a[i - 1];
}
if (360 - s > 0)
gcd = __gcd(gcd, 360 - s);
return (360 / gcd) - n;
}
int main()
{
int arr[] = { 30, 60, 180 };
int n = sizeof(arr) / sizeof(arr[0]);
cout << minimumCuts(arr, n);
return 0;
}
|
Java
import java.util.Arrays;
class GFG
{
static int findgcd(int a, int b)
{
if (b == 0)
return a;
return findgcd(b, a % b);
}
static int minimumCuts(int a[], int n)
{
Arrays.sort(a);
int gcd = a[1] - a[0];
int s = gcd;
for (int i = 2; i < n; i++)
{
gcd = findgcd(gcd, a[i] - a[i - 1]);
s += a[i] - a[i - 1];
}
if (360 - s > 0)
gcd = findgcd(gcd, 360 - s);
return (360 / gcd) - n;
}
public static void main(String[] args)
{
int[] arr = new int[] { 30, 60, 180 };
int n = arr.length;
System.out.println(minimumCuts(arr, n));
}
}
|
Python 3
import math
def minimumCuts(a, n):
a.sort()
gcd = a[1] - a[0]
s = gcd
for i in range(2,n) :
gcd = math.gcd(gcd, a[i] - a[i - 1])
s += a[i] - a[i - 1]
if (360 - s > 0):
gcd = math.gcd(gcd, 360 - s)
return (360 // gcd) - n
if __name__ == "__main__":
arr = [ 30, 60, 180 ]
n = len(arr)
print(minimumCuts(arr, n))
|
C#
using System;
class GFG
{
static int findgcd(int a, int b)
{
if (b == 0)
return a;
return findgcd(b, a % b);
}
static int minimumCuts(int []a, int n)
{
Array.Sort(a);
int gcd = a[1] - a[0];
int s = gcd;
for (int i = 2; i < n; i++)
{
gcd = findgcd(gcd, a[i] - a[i - 1]);
s += a[i] - a[i - 1];
}
if (360 - s > 0)
gcd = findgcd(gcd, 360 - s);
return (360 / gcd) - n;
}
static void Main()
{
int[] arr = new int[] { 30, 60, 180 };
int n = arr.Length;
Console.WriteLine(minimumCuts(arr, n));
}
}
|
PHP
<?php
function findgcd($a, $b)
{
if ($b == 0)
return $a;
return findgcd($b, $a % $b);
}
function minimumCuts($a, $n)
{
sort($a);
$gcd = $a[1] - $a[0];
$s = $gcd;
for ($i = 2; $i < $n; $i++)
{
$gcd = findgcd($gcd, $a[$i] - $a[$i - 1]);
$s += $a[$i] - $a[$i - 1];
}
if (360 - $s > 0)
$gcd = findgcd($gcd, 360 - $s);
return (360 / $gcd) - $n;
}
$arr = array(30, 60, 180);
$n = sizeof($arr);
echo (minimumCuts($arr, $n));
?>
|
Javascript
<script>
function findgcd(a , b)
{
if (b == 0)
return a;
return findgcd(b, a % b);
}
function minimumCuts(a, n)
{
a.sort();
var gcd = a[1] - a[0];
var s = gcd;
for (i = 2; i < n; i++) {
gcd = findgcd(gcd, a[i] - a[i - 1]);
s += a[i] - a[i - 1];
}
if (360 - s > 0)
gcd = findgcd(gcd, 360 - s);
return (360 / gcd) - n;
}
var arr = [ 30, 60, 180 ];
var n = arr.length;
document.write(minimumCuts(arr, n));
</script>
|
Time complexity: O(nlogn), since the sorting best algorithm takes (nlogn) times to sort the array.
Auxiliary Space: O(1), since no extra space has been taken.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...