Minimum number of changes required to make the given array an AP
Last Updated :
31 Aug, 2022
Given an array arr[] of 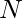 integers and a number
integers and a number  . You can change any element of the array to an integer. The task is to find the minimum number of change(s) required to make the given array an Arithmetic Progression with the common difference
. You can change any element of the array to an integer. The task is to find the minimum number of change(s) required to make the given array an Arithmetic Progression with the common difference  .
.
Examples:
Input : N = 4, d = 2
arr[] = {1, 2, 4, 6}
Output : 1
Explanation: change a[0]=0.
So, new sequence is 0, 2, 4, 6 which is an AP.
Input : N = 5, d = 1
arr[] = {1, 3, 3, 4, 6}
Output : 2
Explanation: change a[1]=2 and a[4]=5.
So, new sequence is 1, 2, 3, 4, 5 which is an AP.
The idea to solve this problem is to observe that the formulae for the n-th term in an AP are:
an = a0 + (n-1)*d
Where, a0 is the first term
and d is the common difference.
We are given the values of 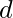 and an. So, we will find the value of a0 for all values of i, where 1<=i<=n and store the frequency of occurrences of a0 for different values of i.
and an. So, we will find the value of a0 for all values of i, where 1<=i<=n and store the frequency of occurrences of a0 for different values of i.
Now, the minimum number of elements needed to be changed is:
n - (maximum frequency of a0)
Where maximum frequency of a0 signifies the total number of elements in the array for which the value of the first term in the AP is the same.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minimumChanges(int arr[], int n, int d)
{
int maxFreq = INT_MIN;
unordered_map<int, int> freq;
for (int i = 0; i < n; ++i) {
int a0 = arr[i] - (i)*d;
if (freq.find(a0) != freq.end()) {
freq[a0]++;
}
else
freq.insert(make_pair(a0, 1));
if (freq[a0] > maxFreq)
maxFreq = freq[a0];
}
return (n - maxFreq);
}
int main()
{
int n = 5, d = 1;
int arr[] = { 1, 3, 3, 4, 6 };
cout << minimumChanges(arr, n, d);
return 0;
}
|
Java
import java.util.*;
class GFG {
static int minimumChanges(int arr[],
int n, int d)
{
int maxFreq = -1;
HashMap<Integer,
Integer>
freq = new HashMap<Integer,
Integer>();
for (int i = 0; i < n; ++i) {
int a0 = arr[i] - (i)*d;
if (freq.containsKey(a0)) {
freq.put(a0, freq.get(a0) + 1);
}
else
freq.put(a0, 1);
if (freq.get(a0) > maxFreq)
maxFreq = freq.get(a0);
}
return (n - maxFreq);
}
public static void main(String args[])
{
int n = 5, d = 1;
int arr[] = { 1, 3, 3, 4, 6 };
System.out.println(minimumChanges(arr, n, d));
}
}
|
Python3
def minimumChanges(arr, n, d):
maxFreq = -2147483648
freq = {}
for i in range(n):
a0 = arr[i] - i * d
if a0 in freq:
freq[a0] += 1
else:
freq[a0] = 1
if freq[a0] > maxFreq:
maxFreq = freq[a0]
return (n-maxFreq)
n = 5
d = 1
arr = [1, 3, 3, 4, 6 ]
ans = minimumChanges(arr, n, d)
print(ans)
|
C#
using System;
using System.Collections.Generic;
class GFG {
static int minimumChanges(int[] arr,
int n, int d)
{
int maxFreq = -1;
Dictionary<int, int> freq = new Dictionary<int, int>();
for (int i = 0; i < n; ++i) {
int a0 = arr[i] - (i)*d;
if (freq.ContainsKey(a0)) {
var obj = freq[a0];
freq.Remove(a0);
freq.Add(a0, obj + 1);
}
else
freq.Add(a0, 1);
if (freq[a0] > maxFreq)
maxFreq = freq[a0];
}
return (n - maxFreq);
}
public static void Main(String[] args)
{
int n = 5, d = 1;
int[] arr = { 1, 3, 3, 4, 6 };
Console.WriteLine(minimumChanges(arr, n, d));
}
}
|
PHP
<?php
function minimumChanges(&$arr, $n, $d)
{
$maxFreq = PHP_INT_MIN;
$freq = array();
for ($i = 0; $i < $n; ++$i)
{
$a0 = $arr[$i] - ($i) * $d;
if(array_search($a0, $freq))
{
$freq[$a0]++;
}
else
$freq[$a0] = 1;
if ($freq[$a0] > $maxFreq)
$maxFreq = $freq[$a0];
}
return ($n - $maxFreq);
}
$n = 5;
$d = 1;
$arr = array( 1, 3, 3, 4, 6 );
echo minimumChanges($arr, $n, $d);
?>
|
Javascript
<script>
function minimumChanges(arr,n,d)
{
let maxFreq = -1;
let freq = new Map();
for (let i = 0; i < n; ++i) {
let a0 = arr[i] - (i)*d;
if (freq.has(a0)) {
freq.set(a0, freq.get(a0) + 1);
}
else
freq.set(a0, 1);
if (freq.get(a0) > maxFreq)
maxFreq = freq.get(a0);
}
return (n - maxFreq);
}
let n = 5, d = 1;
let arr=[ 1, 3, 3, 4, 6];
document.write(minimumChanges(arr, n, d));
</script>
|
Complexity Analysis:
- Time Complexity: O(N)
- Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...