Minimum number of deletions to make a string palindrome | Set 2

Given a string A, compute the minimum number of characters you need to delete to make resulting string a palindrome.
Examples:

Input : baca
Output : 1

Input : geek
Output : 2

We have discussed one approach in below post. 
Minimum number of deletions to make a string palindrome
Below approach will use modified Levenshtein distance. We consider modified Levenshtein (considering only deletions) both original string and its reverse.

C++

// CPP program to find minimum deletions to make
// palindrome.
#include <bits/stdc++.h>
using namespace std;


int getLevenstein(string const& input)
{
    // Find reverse of input string
    string revInput(input.rbegin(), input.rend());

    // Create a DP table for storing edit distance
    // of string and reverse.
    int n = input.size();
    vector<vector<int> > dp(n + 1, vector<int>(n + 1, -1));
    for (int i = 0; i <= n; ++i) {
        dp[0][i] = i;
        dp[i][0] = i;
    }

    // Find edit distance between input and revInput
    // considering only delete operation.
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            if (input[i - 1] == revInput[j - 1])
                dp[i][j] = dp[i - 1][j - 1];
            else
                dp[i][j] = 1 + min({ dp[i - 1][j], dp[i][j - 1] });
        }
    }

    /*Go from bottom left to top right and find the minimum*/
    int res = numeric_limits<int>::max();
    for (int i = n, j = 0; i >= 0; --i, ++j) {
        res = min(res, dp[i][j]);
        if (i < n)
            res = min(res, dp[i + 1][j]);
        if (i > 0)
            res = min(res, dp[i - 1][j]);
    }
    return res;
}

// Driver code
int main()
{
    string input("myfirstgeekarticle");
    cout << getLevenstein(input);
    return 0;
}

Java

// Java program to find minimum deletions to make
// palindrome.
import java.io.*;
import java.util.*;

class GFG
{

    static int getLevenstein(StringBuilder input)
    {
        StringBuilder revInput = new StringBuilder(input);

        // Find reverse of input string
        revInput = revInput.reverse();

        // Create a DP table for storing edit distance
        // of string and reverse.
        int n = input.length();
        int[][] dp = new int[n + 1][n + 1];
        for (int i = 0; i <= n; ++i)
        {
            dp[0][i] = i;
            dp[i][0] = i;
        }

        // Find edit distance between input and revInput
        // considering only delete operation.
        for (int i = 1; i <= n; ++i)
        {
            for (int j = 1; j <= n; ++j)
            {
                if (input.charAt(i - 1) == revInput.charAt(j - 1))
                    dp[i][j] = dp[i - 1][j - 1];
                else
                    dp[i][j] = 1 + Math.min(dp[i - 1][j], dp[i][j - 1]);
            }
        }

        /* Go from bottom left to top right and find the minimum */
        int res = Integer.MAX_VALUE;
        for (int i = n, j = 0; i >= 0; i--, j++)
        {
            res = Math.min(res, dp[i][j]);
            if (i < n)
                res = Math.min(res, dp[i + 1][j]);
            if (i > 0)
                res = Math.min(res, dp[i - 1][j]);
        }
        return res;
    }

    // Driver Code
    public static void main(String[] args)
    {
        StringBuilder input = new StringBuilder("myfirstgeekarticle");
        System.out.println(getLevenstein(input));
    }
}

// This code is contributed by
// sanjeev2552

Python3

# Python3 program to find minimum deletions
# to make palindrome.
INT_MAX = 99999999999

def getLevenstein(inpt):

    # Find reverse of input string
    revInput = inpt[::-1]

    # Create a DP table for storing
    # edit distance of string and reverse.
    n = len(inpt)
    dp = [[-1 for _ in range(n + 1)]
              for __ in range(n + 1)]
    for i in range(n + 1):
        dp[0][i] = i
        dp[i][0] = i

    # Find edit distance between
    # input and revInput considering
    # only delete operation.
    for i in range(1, n + 1):
        for j in range(1, n + 1):
            if inpt[i - 1] == revInput[j - 1]:
                dp[i][j] = dp[i - 1][j - 1]
            else:
                dp[i][j] = 1 + min(dp[i - 1][j],
                                   dp[i][j - 1])

    # Go from bottom left to top right
    # and find the minimum
    res = INT_MAX
    i, j = n, 0
    while i >= 0:
        res = min(res, dp[i][j])
        if i < n:
            res = min(res, dp[i + 1][j])
        if i > 0:
            res = min(res, dp[i - 1][j])
        i -= 1
        j += 1
    return res

# Driver Code
if __name__ == "__main__":
    inpt = "myfirstgeekarticle"
    print(getLevenstein(inpt))

# This code is contributed
# by vibhu4agarwal

C#

// C# program to find minimum deletions to make
// palindrome.
using System;

class GFG
{
    static int getLevenstein(String input)
    {

        // Find reverse of input string
        String revInput = Reverse(input);

        // Create a DP table for storing edit distance
        // of string and reverse.
        int n = input.Length;
        int[,] dp = new int[n + 1, n + 1];
        for (int i = 0; i <= n; ++i)
        {
            dp[0, i] = i;
            dp[i, 0] = i;
        }

        // Find edit distance between input and revInput
        // considering only delete operation.
        for (int i = 1; i <= n; ++i)
        {
            for (int j = 1; j <= n; ++j)
            {
                if (input[i - 1] == revInput[j - 1])
                    dp[i, j] = dp[i - 1, j - 1];
                else
                    dp[i, j] = 1 + Math.Min(dp[i - 1, j],
                                            dp[i, j - 1]);
            }
        }

        /* Go from bottom left to top right
        and find the minimum */
        int res = int.MaxValue;
        for (int i = n, j = 0; i >= 0; i--, j++)
        {
            res = Math.Min(res, dp[i, j]);
            if (i < n)
                res = Math.Min(res, dp[i + 1, j]);
            if (i > 0)
                res = Math.Min(res, dp[i - 1, j]);
        }
        return res;
    }
    static String Reverse(String input)
    {
        char[] a = input.ToCharArray();
        int l, r = a.Length - 1;
        for (l = 0; l < r; l++, r--)
        {
            char temp = a[l];
            a[l] = a[r];
            a[r] = temp;
        }
        return String.Join("",a);
    }

    // Driver Code
    public static void Main(String[] args)
    {
        String input = "myfirstgeekarticle";
        Console.WriteLine(getLevenstein(input));
    }
}

// This code is contributed by 29AjayKumar

Javascript

<script>
// Javascript program to find minimum deletions to make
// palindrome.
function getLevenstein(input)
{
    let revInput = (input).split("");

        // Find reverse of input string
        revInput = revInput.reverse();

        // Create a DP table for storing edit distance
        // of string and reverse.
        let n = input.length;
        let dp = new Array(n + 1);
        for(let i = 0; i < n + 1; i++)
        {
            dp[i] = new Array(n+1);
            for(let j = 0; j < n + 1; j++)
                dp[i][j] = 0;
        }
        for (let i = 0; i <= n; ++i)
        {
            dp[0][i] = i;
            dp[i][0] = i;
        }

        // Find edit distance between input and revInput
        // considering only delete operation.
        for (let i = 1; i <= n; ++i)
        {
            for (let j = 1; j <= n; ++j)
            {
                if (input[i - 1] == revInput[j - 1])
                    dp[i][j] = dp[i - 1][j - 1];
                else
                    dp[i][j] = 1 + Math.min(dp[i - 1][j], dp[i][j - 1]);
            }
        }

        /* Go from bottom left to top right and find the minimum */
        let res = Number.MAX_VALUE;
        for (let i = n, j = 0; i >= 0; i--, j++)
        {
            res = Math.min(res, dp[i][j]);
            if (i < n)
                res = Math.min(res, dp[i + 1][j]);
            if (i > 0)
                res = Math.min(res, dp[i - 1][j]);
        }
        return res;
}

// Driver Code
let input = ("myfirstgeekarticle");
document.write(getLevenstein(input));

// This code is contributed by rag2127
</script>

Output:

12

Time complexity: O() 
Space complexity: O() 
where 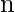is length of string
Why is it working? 
To understand it we need to start from the very beginning of how we create dp[][], for example for word “geek”, it initially looks like this:

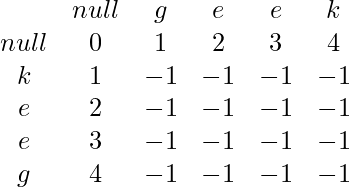
Both 1st row and 1st column are filled with number 1..4 as this is the number of modifications needed to create empty string, i.e: 
[0][1] == 1, to create empty string from letter ‘g’ remove this one letter 
[0][2] == 2, to create empty string from letters “ge”, remove both those letters, etc. 
The same story for first column: 
[1][0] == 1, to create empty string from letter ‘k’ remove this one letter 
[2][0] == 2, to create empty string from letters “ke”, remove both those letters, etc.
Now, we are using dynamic programming approach to get the minimum number of modifications to get every other substring to become second substring, and at the end out dp[][] looks like this:

So for example minimum number of modifications to get substring ‘gee’ from ‘kee’ is 2. So far so good but this algorithm is doing two things, it is both inserting and deleting characters, and we are only interested in number of removals. So let’s one more time take a look at our resulting array, for example at entry [4][1], this entry states: 
[4][1] – to make string ‘g’ from string “keeg” we need to perform 3 modifications(which is just delete chars “kee”) 
[3][2] – to make string “ge” from “kee” we need to perform 3 modifications also by removing from first string ‘g’ and from second ‘ke’ 
So basically every time we will be moving diagonally up, from left corner we will get number of removals to get the same substring backwards. Thing to notice here is that it is like having on string two pointers, one moving from beginning and other from end. Very important spot is that strings do not necessary has to have even number of characters, so this is the reason we also has to check upper and lower values in dp[][].