Minimum insertions to make a Co-prime array
Last Updated :
10 Oct, 2022
Given an array of N elements, find the minimum number of insertions to convert the given array into a co-prime array. Print the resultant array also.
Co-prime Array : An array in which every pair of adjacent elements are co-primes. i.e, 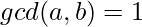 .
.
Examples :
Input : A[] = {2, 7, 28}
Output : 1
Explanation :
Here, 1st pair = {2, 7} are co-primes( gcd(2, 7) = 1).
2nd pair = {7, 28} are not co-primes, insert 9
between them. gcd(7, 9) = 1 and gcd(9, 28) = 1.
Input : A[] = {5, 10, 20}
Output : 2
Explanation :
Here, there is no pair which are co-primes.
Insert 7 between (5, 10) and 1 between (10, 20).
Observe that to make a pair to become co-primes we have to insert a number which makes the newly formed pairs co-primes. So, we have to check every adjacent pair for their co-primality and insert a number if required. Now, what is the number that should be inserted? Let us take two numbers a and b. If any of a or b is 1, then GCD(a, b) = 1. So, we can insert ONE(1) at every pair. For efficiency we use euler’s gcd function .
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void printResult(int arr[], int n)
{
int count = 0;
for (int i = 1; i < n; i++)
if (__gcd(arr[i], arr[i - 1]) != 1)
count++;
cout << count << endl;
cout << arr[0] << " ";
for (int i = 1; i < n; i++)
{
if (__gcd(arr[i], arr[i - 1]) != 1)
cout << 1 << " ";
cout << arr[i] << " ";
}
}
int main()
{
int A[] = { 5, 10, 20 };
int n = sizeof(A) / sizeof(A[0]);
printResult(A, n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int gcd(int a, int b)
{
if (a == 0 || b == 0)
return 0;
if (a == b)
return a;
if (a > b)
return gcd(a-b, b);
return gcd(a, b-a);
}
static void printResult(int arr[], int n)
{
int count = 0;
for (int i = 1; i < n; i++)
if (gcd(arr[i], arr[i - 1]) != 1)
count++;
System.out.println(count );
System.out.print (arr[0] + " ");
for (int i = 1; i < n; i++)
{
if (gcd(arr[i], arr[i - 1]) != 1)
System.out.print( 1 + " ");
System.out.print(arr[i] + " ");
}
}
public static void main(String args[])
{
int A[] = { 5, 10, 20 };
int n = A.length;
printResult(A, n);
}
}
|
Python3
from fractions import gcd
def printResult(arr, n):
count = 0
for i in range(1,n):
if (gcd(arr[i], arr[i - 1]) != 1):
count+=1
print(count)
print( arr[0], end = " ")
for i in range(1,n):
if (gcd(arr[i], arr[i - 1]) != 1):
print(1, end = " ")
print(arr[i] , end = " ")
A = [ 5, 10, 20 ]
n = len(A)
printResult(A, n)
|
C#
using System;
class GFG {
static int gcd(int a, int b)
{
if (a == 0 || b == 0)
return 0;
if (a == b)
return a;
if (a > b)
return gcd(a - b, b);
return gcd(a, b - a);
}
static void printResult(int[] arr, int n)
{
int count = 0;
for (int i = 1; i < n; i++)
if (gcd(arr[i], arr[i - 1]) != 1)
count++;
Console.WriteLine(count);
Console.Write(arr[0] + " ");
for (int i = 1; i < n; i++) {
if (gcd(arr[i], arr[i - 1]) != 1)
Console.Write(1 + " ");
Console.Write(arr[i] + " ");
}
}
public static void Main()
{
int[] A = { 5, 10, 20 };
int n = A.Length;
printResult(A, n);
}
}
|
PHP
<?php
function gcd($a, $b)
{
if ($a == 0 || $b == 0)
return 0;
if ($a == $b)
return $a;
if ($a > $b)
return gcd($a - $b, $b);
return gcd($a, $b - $a);
}
function printResult($arr, $n)
{
$count = 0;
for ($i = 1; $i < $n; $i++)
if (gcd($arr[$i],
$arr[$i - 1]) != 1)
$count++;
echo $count, "\n";
echo $arr[0] , " ";
for ($i = 1; $i < $n; $i++)
{
if (gcd($arr[$i],
$arr[$i - 1]) != 1)
echo 1 , " ";
echo $arr[$i] , " ";
}
}
$A = array(5, 10, 20);
$n = sizeof($A);
printResult($A, $n);
?>
|
Javascript
<script>
function gcd(a, b)
{
if (a == 0 || b == 0)
return 0;
if (a == b)
return a;
if (a > b)
return gcd(a - b, b);
return gcd(a, b - a);
}
function printResult(arr, n)
{
let count = 0;
for(let i = 1; i < n; i++)
if (gcd(arr[i], arr[i - 1]) != 1)
count++;
document.write(count + "</br>");
document.write(arr[0] + " ");
for(let i = 1; i < n; i++)
{
if (gcd(arr[i], arr[i - 1]) != 1)
document.write(1 + " ");
document.write(arr[i] + " ");
}
}
let A = [ 5, 10, 20 ];
let n = A.length;
printResult(A, n);
</script>
|
Time Complexity: O(n log(Ai)), for using __gcd function
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...