Minimum deletions from string to reduce it to string with at most 2 unique characters

Given a string 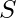containing lowercase English alphabets. The task is to find the minimum number of characters needed to be removed so that the remaining string contains at most 2 unique characters.

Note: The final string can have duplicate characters. The task is only to reduce the string with minimum deletions such that there can be a maximum of 2 unique characters in the resultant string.

Examples:

Input: S = “geeksforgeeks” 
Output: 7 
After removing 7 characters, the final string will be “geegee”

Input: S = “helloworld” 
Output: 5 

Approach:

First count the occurrences of each character within the given string, then just select two characters with the maximum occurrence, i.e. the two most frequently occurring characters in the string. And the result will be:  

String length – (Occurrence of 1st most frequent character + Occurrence of 2nd most frequent character)

Below is the implementation of the above approach:  

C++

// C++ implementation of the above approach

#include<bits/stdc++.h>
using namespace std;

// Function to find the minimum deletions
int check(string s)
{

    int i, j;
    // Array to store the occurrences
    // of each characters
    int fr[26] = {0} ;

    // Length of the string
    int n = s.size() ;
    for(i = 0; i < n; i++)
    {

        // ASCII of the character
        char x = s[i] ;

        // Increasing the frequency for this character
        fr[x-'a'] += 1 ;

    }


    int minimum = INT_MAX;

    for(i = 0 ; i < 26; i++)
    {
        for( j = i + 1;j < 26; j++)
        {

            // Choosing two character
            int z = fr[i] + fr[j] ;

            // Finding the minimum deletion
            minimum = min(minimum, n - z) ;
        }
    }

    return minimum ;
}

/* Driver code */
int main()
{
    string s ="geeksforgeeks" ;
    cout << check(s) ;
}

// This code is contributed by ihritik

Java

// Java implementation of the above approach

public class GFG{

// Function to find the minimum deletions
static int check(String s)
{

    int i,j;
    // Array to store the occurrences
    // of each characters
    int fr[] = new int[26] ;

    // Length of the string
    int n = s.length() ;
    for(i = 0; i < n; i++)
    {

        // ASCII of the character
        char x = s.charAt(i) ;

        // Increasing the frequency for this character
        fr[x-'a'] += 1 ;

    }


    int minimum = Integer.MAX_VALUE;

    for(i = 0 ; i < 26; i++)
    {
        for( j = i + 1;j < 26; j++)
        {

            // Choosing two character
            int z = fr[i] + fr[j] ;

            // Finding the minimum deletion
            minimum = Math.min(minimum, n-z) ;
        }
    }

    return minimum ;
}

    /* Driver program to test above functions */
     public static void main(String []args){

        String s ="geeksforgeeks" ;
        System.out.println(check(s)) ;

        }
    // This code is contributed by ANKITRAI1
}

Python3

# Python3 implementation of the above approach

# Function to find the minimum deletions
def check(s):

    # Array to store the occurrences
    # of each characters
    fr =[0]*26

    # Length of the string
    n = len(s)
    for i in range(n):

        # ASCII of the character
        x = ord(s[i])

        # Increasing the frequency for this character
        fr[x-97] += 1

    minimum = 99999999999

    for i in range(26):
        for j in range(i + 1, 26):

            # Choosing two character
            z = fr[i] + fr[j]

            # Finding the minimum deletion
            minimum = min(minimum, n-z)

    return minimum

# Driver code
s ="geeksforgeeks"
print(check(s))

C#

// C# implementation of the above approach

using System;
public class GFG{

// Function to find the minimum deletions
static int check(string s)
{

    int i,j;
    // Array to store the occurrences
    // of each characters
    int[] fr = new int[26] ;

    // Length of the string
    int n = s.Length ;
    for(i = 0; i < n; i++)
    {

        // ASCII of the character
        char x = s[i] ;

        // Increasing the frequency for this character
        fr[x-'a'] += 1 ;

    }


    int minimum = int.MaxValue;

    for(i = 0 ; i < 26; i++)
    {
        for( j = i + 1;j < 26; j++)
        {

            // Choosing two character
            int z = fr[i] + fr[j] ;

            // Finding the minimum deletion
            minimum = Math.Min(minimum, n-z) ;
        }
    }

    return minimum ;
}

    /* Driver program to test above functions */
     public static void Main(){

        string s ="geeksforgeeks" ;
        Console.Write(check(s)) ;

        }
}

Javascript

<script>

// Javascript implementation of the above approach

// Function to find the minimum deletions
function check(s)
{

    var i, j;
    // Array to store the occurrences
    // of each characters
    var fr = Array(26).fill(0);

    // Length of the string
    var n = s.length ;
    for(i = 0; i < n; i++)
    {

        // ASCII of the character
        var x = s[i] ;

        // Increasing the frequency for this character
        fr[x.charCodeAt(0) -'a'.charCodeAt(0)] += 1 ;

    }


    var minimum = 10000000000;

    for(i = 0 ; i < 26; i++)
    {
        for( j = i + 1;j < 26; j++)
        {

            // Choosing two character
            var z = fr[i] + fr[j] ;

            // Finding the minimum deletion
            minimum = Math.min(minimum, n - z) ;
        }
    }

    return minimum ;
}

/* Driver code */
var s ="geeksforgeeks" ;
document.write( check(s));

</script>

Output

7

Time Complexity: O(N), where N is the length of the given string.
Auxiliary Space: O(1) because it is using constant space.