Minimum count of elements that sums to a given number
Last Updated :
10 Mar, 2022
Given infinite number of elements of form 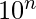 and
and 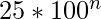 ( n >= 0 ). The task is to find the minimum count of elements chosen such that there sum is equal to K.
( n >= 0 ). The task is to find the minimum count of elements chosen such that there sum is equal to K.
Examples:
Input : K = 48
Output : 6
elements chosen are: (1 + 1 + 1 + 10 + 10 + 25)
Input : 69
Output : 9
elements chosen are: (1 + 1 + 1 + 1 + 10 + 10 + 10 + 10 + 25)
Approach:
There are infinite number of the following elements :
1, 10, 25, 100, 1000, 2500, 10000, 100000, 250000 … and so on.
Greedy Approach won’t work here. For K = 66, by Greedy Approach minimum count will be 9 and chosen elements are 25 + 25 + 10 + 1 + 1 + 1 + 1 + 1 + 1 = 66. But its optimum answer is 6 when these elements are chosen: 25 + 10 + 10 + 10 + 10 + 1 = 66. So, Dynamic Programming will work here. But simple DP cannot be applied because K can go upto 10^9 .
Dynamic Programming approach:
- Precompute the minimum no. of elements chosen that constitutes sum upto 99 and store it in memo array.
- Also, sums upto 99 can only be formed by the combinations of 1, 10 and 25.
- Starting from end of K, iterate over each last 2 digits to find minimum no. of elements chosen that will sum to last two digits.
- Sum them all to find the minimum count.
Illustration of the above approach:
Let’s take K = 250166
Let min_count = 0, last 2 digits = 66
add minimum number of elements to min_count that sums to 66 (it is calculated from memo array
that we have precomputed).
min_count = min_count + 6,
Now, min_count = 6, last 2 digits = 01
add minimum number of elements to min_count sums to 1.
min_count = min_count + 1,
Now, min_count = 7, last 2 digits = 25
add minimum number of elements to min_count sums to 25.
min_count = min_count + 1,
Now, min_count = 8.
So, minimum number of elements chosen that sums to 250166 is 8.
Optimal chosen Elements are (250000, 100, 25, 10, 10, 10, 10, 1)
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int minCount(int K)
{
int memo[100];
for (int i = 0; i < 100; i++) {
memo[i] = INT_MAX;
}
memo[0] = 0;
for (int i = 1; i < 100; i++) {
memo[i] = min(memo[i - 1] + 1, memo[i]);
}
for (int i = 10; i < 100; i++) {
memo[i] = min(memo[i - 10] + 1, memo[i]);
}
for (int i = 25; i < 100; i++) {
memo[i] = min(memo[i - 25] + 1, memo[i]);
}
long min_count = 0;
while (K > 0) {
min_count += memo[K % 100];
K /= 100;
}
return min_count;
}
int main()
{
int K = 69;
cout << minCount(K) << endl;
return 0;
}
|
Java
class GFG
{
static int minCount(int K)
{
int memo[] = new int[100];
for (int i = 0; i < 100; i++)
{
memo[i] = Integer.MAX_VALUE;
}
memo[0] = 0;
for (int i = 1; i < 100; i++)
{
memo[i] = Math.min(memo[i - 1] + 1, memo[i]);
}
for (int i = 10; i < 100; i++)
{
memo[i] = Math.min(memo[i - 10] + 1, memo[i]);
}
for (int i = 25; i < 100; i++)
{
memo[i] = Math.min(memo[i - 25] + 1, memo[i]);
}
int min_count = 0;
while (K > 0)
{
min_count += memo[K % 100];
K /= 100;
}
return min_count;
}
public static void main (String[] args)
{
int K = 69;
System.out.println(minCount(K));
}
}
|
Python3
def minCount(K):
memo=[10**9 for i in range(100)]
memo[0] = 0
for i in range(1,100):
memo[i] = min(memo[i - 1] + 1, memo[i])
for i in range(10,100):
memo[i] = min(memo[i - 10] + 1, memo[i])
for i in range(25,100):
memo[i] = min(memo[i - 25] + 1, memo[i])
min_count = 0
while (K > 0):
min_count += memo[K % 100]
K //= 100
return min_count
K = 69
print(minCount(K))
|
C#
using System;
class GFG
{
static int minCount(int K)
{
int []memo = new int[100];
for (int i = 0; i < 100; i++)
{
memo[i] = int.MaxValue;
}
memo[0] = 0;
for (int i = 1; i < 100; i++)
{
memo[i] = Math.Min(memo[i - 1] + 1, memo[i]);
}
for (int i = 10; i < 100; i++)
{
memo[i] = Math.Min(memo[i - 10] + 1, memo[i]);
}
for (int i = 25; i < 100; i++)
{
memo[i] = Math.Min(memo[i - 25] + 1, memo[i]);
}
int min_count = 0;
while (K > 0)
{
min_count += memo[K % 100];
K /= 100;
}
return min_count;
}
static public void Main ()
{
int K = 69;
Console.WriteLine(minCount(K));
}
}
|
Javascript
<script>
function minCount(K)
{
let memo = new Array(100);
for (let i = 0; i < 100; i++)
{
memo[i] = Number.MAX_VALUE;
}
memo[0] = 0;
for (let i = 1; i < 100; i++)
{
memo[i] = Math.min(memo[i - 1] + 1, memo[i]);
}
for (let i = 10; i < 100; i++)
{
memo[i] = Math.min(memo[i - 10] + 1, memo[i]);
}
for (let i = 25; i < 100; i++)
{
memo[i] = Math.min(memo[i - 25] + 1, memo[i]);
}
let min_count = 0;
while (K > 0)
{
min_count += memo[K % 100];
K = parseInt(K / 100, 10);
}
return min_count;
}
let K = 69;
document.write(minCount(K));
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...