Minimum cost to reverse edges such that there is path between every pair of nodes
Last Updated :
22 Dec, 2022
Given a connected, directional graph. Each node is connected to exactly two other nodes. There is a weight associated with each edge denoting the cost to reverse its direction. The task is to find the minimum cost to reverse some edges of the graph such that it is possible to go from each node to every other node.
Examples:
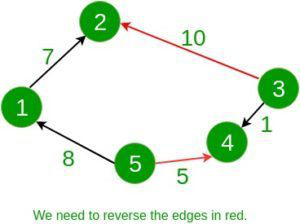
Input:
5
1 2 7
5 1 8
5 4 5
3 4 1
3 2 10
Output: 15
Input:
6
1 5 4
5 3 8
2 4 15
1 6 16
2 3 23
4 6 42
Output: 39
Approach:
- In order to reach from each node to every other node, the graph must form a ring i.e Direct all edges on it in one of 2 directions either clockwise or anti-clockwise. Let us denote the cost of redirecting all the clockwise edges to anticlockwise direction as cost1 and vice versa as cost2. The answer is clearly the minimum of these two costs.
- Maintain two boolean arrays start and end. The start and end arrays denote whether there is an edge starting from or ending at a given node. Whenever we encounter an edge going from node a to node b, we first check the condition if there is an edge already starting from node a or ending at node b. If there is an edge that satisfying the condition, the edge is in the opposite direction to the edge already present. In this case, we update cost2 and store the edge in the opposite direction. Otherwise, we update the cost1. This way we are able to maintain the costs of both orientations. Finally, print the minimum cost.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int minCost(vector<vector<int> >& graph, int n)
{
int cost1 = 0, cost2 = 0;
bool start[n + 1] = { false };
bool end[n + 1] = { false };
for (int i = 0; i < n; i++) {
int a = graph[i][0];
int b = graph[i][1];
int c = graph[i][2];
if (start[a] || end[b]) {
cost2 += c;
start[b] = true;
end[a] = true;
}
else {
cost1 += c;
start[a] = true;
end[b] = true;
}
}
return min(cost1, cost2);
}
int main()
{
int n = 5;
vector<vector<int> > graph = {
{ 1, 2, 7 },
{ 5, 1, 8 },
{ 5, 4, 5 },
{ 3, 4, 1 },
{ 3, 2, 10 }
};
int ans = minCost(graph, n);
cout << ans << '\n';
return 0;
}
|
Java
class GFG
{
static int minCost(int[][] graph, int n)
{
int cost1 = 0, cost2 = 0;
boolean []start = new boolean[n + 1];
boolean []end = new boolean[n + 1];
for (int i = 0; i < n; i++)
{
int a = graph[i][0];
int b = graph[i][1];
int c = graph[i][2];
if (start[a] || end[b])
{
cost2 += c;
start[b] = true;
end[a] = true;
}
else
{
cost1 += c;
start[a] = true;
end[b] = true;
}
}
return Math.min(cost1, cost2);
}
public static void main(String[] args)
{
int n = 5;
int [][]graph = {{ 1, 2, 7 },
{ 5, 1, 8 },
{ 5, 4, 5 },
{ 3, 4, 1 },
{ 3, 2, 10 }};
int ans = minCost(graph, n);
System.out.println(ans);
}
}
|
Python3
def minCost(graph, n):
cost1, cost2 = 0, 0;
start = [False]*(n + 1);
end = [False]*(n + 1);
for i in range(n):
a = graph[i][0];
b = graph[i][1];
c = graph[i][2];
if (start[a] or end[b]):
cost2 += c;
start[b] = True;
end[a] = True;
else:
cost1 += c;
start[a] = True;
end[b] = True;
return min(cost1, cost2);
if __name__ == '__main__':
n = 5;
graph = [[ 1, 2, 7 ],
[ 5, 1, 8 ],
[ 5, 4, 5 ],
[ 3, 4, 1 ],
[ 3, 2, 10 ]];
ans = minCost(graph, n);
print(ans);
|
C#
using System;
class GFG
{
static int minCost(int[,] graph, int n)
{
int cost1 = 0, cost2 = 0;
Boolean []start = new Boolean[n + 1];
Boolean []end = new Boolean[n + 1];
for (int i = 0; i < n; i++)
{
int a = graph[i, 0];
int b = graph[i, 1];
int c = graph[i, 2];
if (start[a] || end[b])
{
cost2 += c;
start[b] = true;
end[a] = true;
}
else
{
cost1 += c;
start[a] = true;
end[b] = true;
}
}
return Math.Min(cost1, cost2);
}
public static void Main(String[] args)
{
int n = 5;
int [,]graph = {{ 1, 2, 7 },
{ 5, 1, 8 },
{ 5, 4, 5 },
{ 3, 4, 1 },
{ 3, 2, 10 }};
int ans = minCost(graph, n);
Console.WriteLine(ans);
}
}
|
Javascript
<script>
function minCost(graph, n) {
let cost1 = 0, cost2 = 0;
let start = new Array(n + 1).fill(false);
let end = new Array(n + 1).fill(false);
for (let i = 0; i < n; i++) {
let a = graph[i][0];
let b = graph[i][1];
let c = graph[i][2];
if (start[a] || end[b]) {
cost2 += c;
start[b] = true;
end[a] = true;
}
else {
cost1 += c;
start[a] = true;
end[b] = true;
}
}
return Math.min(cost1, cost2);
}
let n = 5;
let graph = [
[1, 2, 7],
[5, 1, 8],
[5, 4, 5],
[3, 4, 1],
[3, 2, 10]
];
let ans = minCost(graph, n);
document.write(ans + '<br>');
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(n)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...