Minimum and Maximum number of pairs in m teams of n people
Last Updated :
02 Jul, 2022
There are 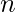 people which are to be grouped into exactly
people which are to be grouped into exactly 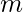 teams such that there is at least one person in each team. All members of a team are friends with each other. Find the minimum and maximum no. of pairs of friends that can be formed by grouping these
teams such that there is at least one person in each team. All members of a team are friends with each other. Find the minimum and maximum no. of pairs of friends that can be formed by grouping these 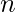 people into exactly
people into exactly 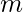 teams.
teams.
Examples:
Input : 5 2
Output : 4 6
For maximum no. of pairs, 1st team contains only 1 member and 2nd team contains 4 people which are friends which each other, so no. of pairs in 1st team + no. of pairs in 2nd team = 0 + 6 = total pairs = 6
For minimum no. of pairs, 1st team contains 2 members and 2nd team contains 3 people which are friends which each other, so no. of pairs in 1st team + no. of pairs in 2nd team = 1 + 3 = total pairs = 4
Input : 2 1
Output : 1 1
Explanation:
First of all, we have to put 1 member in each team to satisfy the constraint. So we are left with  people.
people.
1. For maximum no. of pairs
It can be seen that maximum no. pairs can result only by putting all of the remaining members of the same team. It can be explained as follows:
Consider 2 teams one containing x people and other containing 1 person, now we have to add 1 more person to both the teams, adding him/her to the team of x people increases the no. of pairs by x while adding him to the other team only increases the no. of pairs by 1. Hence, for maximum no. of pairs, we have to put all the remaining people in the same team.
Now the teams distribution for maximum no. of pairs would be something like this:
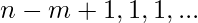
Hence,
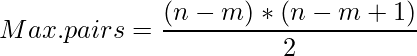
Ex: If a team consists of 3 persons, the 3rd person has 1 and 2 as friends, the 2nd person has 1 as a friend. Therefore, 2+1 = ((3-1)*(3))/2 friends
2. For minimum no. of pairs Now from the same explanation, it can be seen that minimum no. of pairs are obtained when all the persons are distributed equally in the teams. Hence remaining n-m people should be distributed in m teams so that each team contains (n-m)/m more people. Now there are
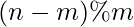
people still remaining which are to be filled 1 in each team (can be seen contrary to the above condition of maximum).
Now the team distribution for minimum no. of pairs would be something like this:
Each team has
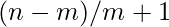
members and
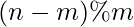
teams have one member extra.
So total no. of pairs = Total no.s of pairs in m teams each of size
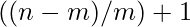
+ No. of pairs formed by adding 1 person in
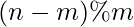
teams which have size
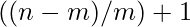
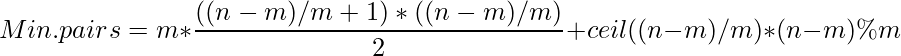
C++
#include <bits/stdc++.h>
using namespace std;
void MinimumMaximumPairs(int n, int m)
{
int max_pairs = ((n - m + 1) * (n - m)) / 2;
int min_pairs = m * (((n - m) / m + 1) * ((n - m) / m)) / 2 +
ceil((n - m) / double(m)) * ((n - m) % m);
cout << "Minimum no. of pairs = " << min_pairs << "\n";
cout << "Maximum no. of pairs = " << max_pairs << "\n";
}
int main()
{
int n = 5, m = 2;
MinimumMaximumPairs(n, m);
return 0;
}
|
Java
import java.io.*;
class GFG {
static void MinimumMaximumPairs(int n, int m)
{
int max_pairs = ((n - m + 1) * (n - m)) / 2;
int min_pairs = m * (((n - m) / m + 1) * ((n - m) / m)) / 2 +
(int)Math.ceil((double)((n - m) /
(double)(m))) * ((n - m) % m);
System.out.println("Minimum no. of pairs = " + min_pairs);
System.out.println("Maximum no. of pairs = " + max_pairs);
}
public static void main (String[] args) {
int n = 5, m = 2;
MinimumMaximumPairs(n, m);
}
}
|
Python3
from math import ceil
def MinimumMaximumPairs(n, m) :
max_pairs = ((n - m + 1) * (n - m)) // 2;
min_pairs = (m * (((n - m) // m + 1) *
((n - m) // m)) // 2 +
ceil((n - m) / (m)) *
((n - m) % m))
print("Minimum no. of pairs = ", min_pairs)
print("Maximum no. of pairs = " , max_pairs)
if __name__ == "__main__" :
n ,m= 5, 2
MinimumMaximumPairs(n, m)
|
C#
using System;
class GFG
{
static void MinimumMaximumPairs(int n, int m)
{
int max_pairs = ((n - m + 1) * (n - m)) / 2;
int min_pairs = m * (((n - m) / m + 1) * ((n - m) / m)) / 2 +
(int)Math.Ceiling((double)((n - m) /
(double)(m))) * ((n - m) % m);
Console.WriteLine("Minimum no. of pairs = " + min_pairs);
Console.WriteLine("Maximum no. of pairs = " + max_pairs);
}
public static void Main()
{
int n = 5, m = 2;
MinimumMaximumPairs(n, m);
}
}
|
PHP
<?php
function MinimumMaximumPairs($n, $m)
{
$max_pairs = (($n - $m + 1) * ($n - $m)) / 2;
$min_pairs = $m * (int)((((int)($n - $m) / $m + 1) *
((int)($n - $m) / $m)) / 2) +
(int)ceil(($n - $m) / $m) *
(($n - $m) % $m);
echo("Minimum no. of pairs = " .
"$min_pairs" . "\n");
echo("Maximum no. of pairs = " .
"$max_pairs");
}
$n = 5; $m = 2;
MinimumMaximumPairs($n, $m);
?>
|
Javascript
<script>
function MinimumMaximumPairs(n, m)
{
var max_pairs = parseInt(((n - m + 1) * (n - m)) / 2);
var min_pairs = m * parseInt((((n - m) / m + 1) * ((n - m) / m)) / 2)
+ parseInt( Math.ceil(((n - m) / (m)))) * ((n - m) % m);
document.write("Minimum no. of pairs = " + min_pairs+"<br/>");
document.write("Maximum no. of pairs = " + max_pairs);
}
var n = 5, m = 2;
MinimumMaximumPairs(n, m);
</script>
|
Output
Minimum no. of pairs = 4
Maximum no. of pairs = 6
Time Complexity: 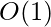
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...